307. Найдите корни уравнения: a) (x-1)(x + 1)(x² + 1) = 10x²-10; б) (x-2)(x + 2)(x² + 4) = &x² - 32: B) (x-4)(x+4)(x² + 16) = 4x² - 196; г) (2х-3)(2х + 3)(4x² + 9) = 10x²-82.
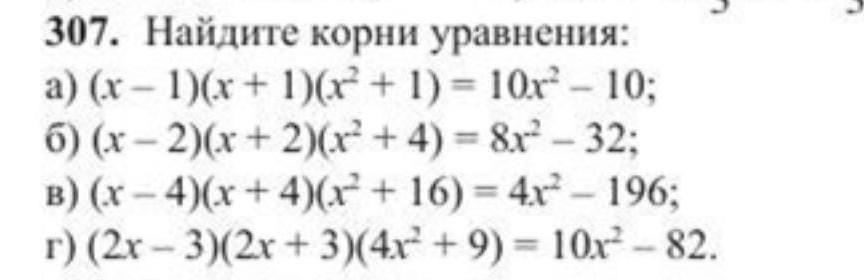
Ответы
Ответ:
а) х₁ = 3; х₂ = -3; х₃ = 1; х₄ = -1
б) х₁ = 2; х₂ = -2
в) х₁ = √10; х₂ = -√10
г) х₁ = √(1/2); х₂ = -√(1/2); х₃ = √(1/8); х₄ = -√(1/8)
Решение:
При решении уравнений, воспользуемся формулой разности квадратов, которая равна произведению разности и суммы двух выражений:
(a - b)(a + b) = a² - b²
a) (x - 1)(x + 1)(x² + 1) = 10x² - 10
(x² - 1)(x² + 1) = 10x² - 10
x⁴ - 1 = 10x² - 10
x⁴ - 10x² + 9 = 0
x² = t
t² - 10t + 9 = 0
D = (-10)² - 4 ∙ 9 = 100 - 36 = 64
t₁ = (10 + √64)/2 = (10 + 8)/2 = 18/2 = 9
t₂ = (10 - √64)/2 = (10 - 8)/2 = 2/2 = 1
x² = t₁ x² = t₂
x² = 9 x² = 1
x = ±3 x = ±1
б) (x - 2)(x + 2)(x² + 4) = 8x² - 32
(x² - 4)(x² + 4) = 8x² - 32
x⁴ - 16 = 8x² - 32
x⁴ - 8x² + 16 = 0
x² = t
t² - 8t + 16 = 0
D = (-8)² - 4 ∙ 16 = 64 - 64 = 0
t = 8/2 = 4
x² = t
x² = 4
x = ±2
в) (x - 4)(x + 4)(x² + 16) = 4x² - 196
(x² - 16)(x² + 16) = 4x² - 196
x⁴ - 256 = 4x² - 196
x⁴ - 4x² - 256 + 196 = 0
x⁴ - 4x² - 60 = 0
x² = t
t² - 4t - 60 = 0
D = (-4)² - 4 ∙ (-60) = 16 + 240 = 256
t₁ = (4 + √256)/2 = (4 + 16)/2 = 20/2 = 10
t₂ = (4 - √256)/2 = (4 - 16)/2 = -12/2 = -6
x² = t₁ x² = t₂
x² = 10 x² = -6
x = ±√10 ∅
г) (2х - 3)(2х + 3)(4x² + 9) = 10x² - 82
(4х² - 9)(4x² + 9) = 10x² - 82
16х⁴ - 81 = 10x² - 82
16х⁴ - 10x² - 81 + 82 = 0
16х⁴ - 10x² + 1 = 0
x² = t
16t² - 10t + 1 = 0
D = (-10)² - 4 ∙ 16 ∙ 1 = 100 - 64 = 36
t₁ = (10 + √36)/(2 ∙ 16) = (10 + 6)/32 = 16/32 = 1/2
t₂ = (10 - √36)/(2 ∙ 16) = (10 - 6)/32 = 4/32 = 1/8
x² = t₁ x² = t₂
x² = 1/2 x² = 1/8
x = ±√(1/2) x = ±√(1/8)
#SPJ1