Предмет: Математика,
автор: dkuznetspv
СРОЧНО ! Высшая математика . Нужен только метод преобразования !!!
Приложения:
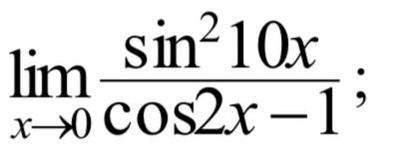
Ответы
Автор ответа:
1
Ответ:
Примечание:
По таблице эквивалентностей:
При
Формула понижения степени:
Пошаговое объяснение:
.
dkuznetspv:
Спасибо большое
Похожие вопросы
Предмет: Математика,
автор: saidarova200
Предмет: Математика,
автор: kerimliayshan7
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: tonykitten35
Предмет: Українська література,
автор: Tomtrinh