Question

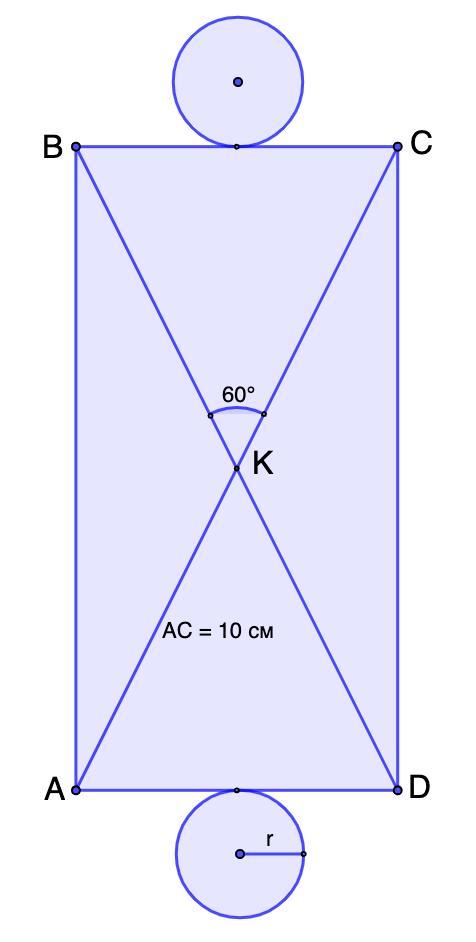
Прямокутник ABCD є розгорткою бічної поверхні циліндра. Діагональ прямокутника дорівнює 10 см, а кут між діагоналями 60 градусів. Знайдіть площу повної поверхні циліндра, якщо більша сторона прямокутника ABCD є висотою циліндра

Answer 1

Ответ:

Площадь полной поверхности цилиндра равна 47,3 см².

Объяснение:

Прямоугольник ABCD является разверткой боковой поверхности цилиндра. Диагональ прямоугольника равна 10 см, а угол между диагоналями 60 градусов. Найдите площадь полной поверхности цилиндра, если большая сторона прямоугольника ABCD является высотой цилиндра.

Дано: ABCD - развертка цилиндра.

АВ - высота цилиндра;

АС = 10 см; ∠ВКС = 60°.

Найти: S полн.

Решение:

Площадь полной поверхности равна сумме площадей боковой поверхности и двух оснований:

S = S бок + 2S осн.

S бок = S (ABCD) = АВ · ВС

S осн = πr²

1. Рассмотрим ΔВКС.

• Диагонали прямоугольника равны и точкой пересечения делятся пополам.

⇒ ВК = КС = 10 : 2 = 5 (см)

ΔВКС - равнобедренный.

• Если угол при вершине равнобедренного треугольника равен 60°, то этот треугольник равносторонний.

⇒ ВС = 5 см.

2. Рассмотрим ΔАВС - прямоугольный.

По теореме Пифагора найдем АВ:

АВ² = АС² - ВС² = 100 - 25 = 75

АВ = √75 = 5√3 (см)

3. Можем найти площадь ABCD.

• Площадь прямоугольника равна произведению смежных сторон.

S(ABCD) = АВ · ВС = 5√3 · 5 = 25√3 (см²)

4. Найдем площадь основания.

Длина окружности основания равна меньшей стороне ABCD.

L = 2πr = ВС =5 см, где L - длина окружности.

или

$\displaystyle 2\pi r=5$ cм.

Найдем радиус:

$\displaystyle r=\frac{5}{2\pi }$  (см)

$\displaystyle S_{OCH}=\pi \cdot \frac{25}{4\pi ^2}=\frac{25}{4\pi }$

5. Найдем площадь полной поверхности цилиндра:

$\displaystyle S = 25\sqrt{3}+2\cdot \frac{25}{4\pi } =25\sqrt{3}+\frac{25}{2\pi } \approx 47,3$  (см²)

Площадь полной поверхности цилиндра равна 47,3 см².

#SPJ1)