Предмет: Алгебра,
автор: Iren245
Ребят, алгебра!!! Это 2 часть моего вопроса по данным уравнениям)) Так же помогите решить с полным объяснением
Приложения:
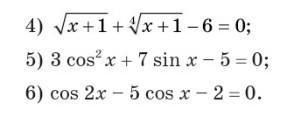
Ответы
Автор ответа:
2
Ответ:
4) Ответ: 15.
5) Ответ:
6) Ответ:
Объяснение:
Решить уравнения:
У нас корни четной степени.
- Подкоренное выражение неотрицательно.
ОДЗ: х + 1 ≥ 0 ⇒ х ≥ -1
Выполним замену переменной:
Получим квадратное уравнение:
По теореме Виета:
Так как t ≥ 0, то t₁ - посторонний корень.
Выполним обратную замену:
Возведем обе части уравнения в 4-ю степень:
Проверим:
Верно!
Ответ: 15.
- Основное тригонометрическое тождество:
- sin²x + cos²x = 1
⇒ cos²x = 1 - sin²x
Выполним замену:
sin x = t
Так как |sin x| ≤ 1, то t₁ - посторонний корень.
Выполним обратную замену:
Ответ:
- Косинус двойного угла:
- cos 2x = 2cos²x - 1
Замена переменной:
Получим квадратное уравнение:
t₁ - посторонний корень.
Выполним обратную замену:
Ответ:
natalyabryukhova:
На здоровье)
Похожие вопросы
Предмет: Английский язык,
автор: aalekc494
Предмет: Физика,
автор: xokyno
Предмет: Биология,
автор: DARIA8218
Предмет: Биология,
автор: 12345677890123456789
Предмет: Математика,
автор: Аноним