Предмет: Алгебра,
автор: Iren245
Ребят, алгебра!!! Помогите решить уравнения с полным объяснением
Приложения:
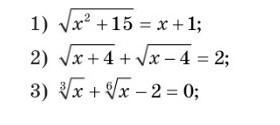
Ответы
Автор ответа:
1
Ответ:
Ответ:
1) 7; 2) ∅ 3) 1.
Объяснение:
Решить уравнения:
Рассмотрим подкоренное выражение:
х² ≥ 0; x² + 15 > 0 ⇒ левая часть положительна, тогда и правая часть положительна.
ОДЗ: х + 1 > 0 ⇒ x > -1
Возведем в квадрат обе части уравнения:
Проверим:
Верно!
Ответ: 7.
Подкоренное выражение неотрицательно.
ОДЗ:
Возведем в квадрат обе части уравнения:
Еще раз возведем в квадрат:
Проверим:
Корень не подходит.
Ответ: ∅
У нас есть корень с показателем в четной степени 6.
ОДЗ: х ≥ 0
Выполним замену переменной:
По теореме Виета корни равны:
Так как t ≥ 0, t₂ - посторонний корень.
Выполним обратную замену:
Проверим:
Верно!
Ответ: 1.
Похожие вопросы
Предмет: Физика,
автор: Pomogitety
Предмет: Химия,
автор: homaula4
Предмет: Английский язык,
автор: evstalena09
Предмет: Биология,
автор: osincevakristina8
Предмет: Українська мова,
автор: vikamuha322