Предмет: Алгебра,
автор: zeynepennazarova
вычислить производные функции f(x) в указанных точках f(x)= 3-x / 2+x
а) x=0
б)x= -3
в)x=3
г)x= -1
срочно! пожалуйста
Приложения:
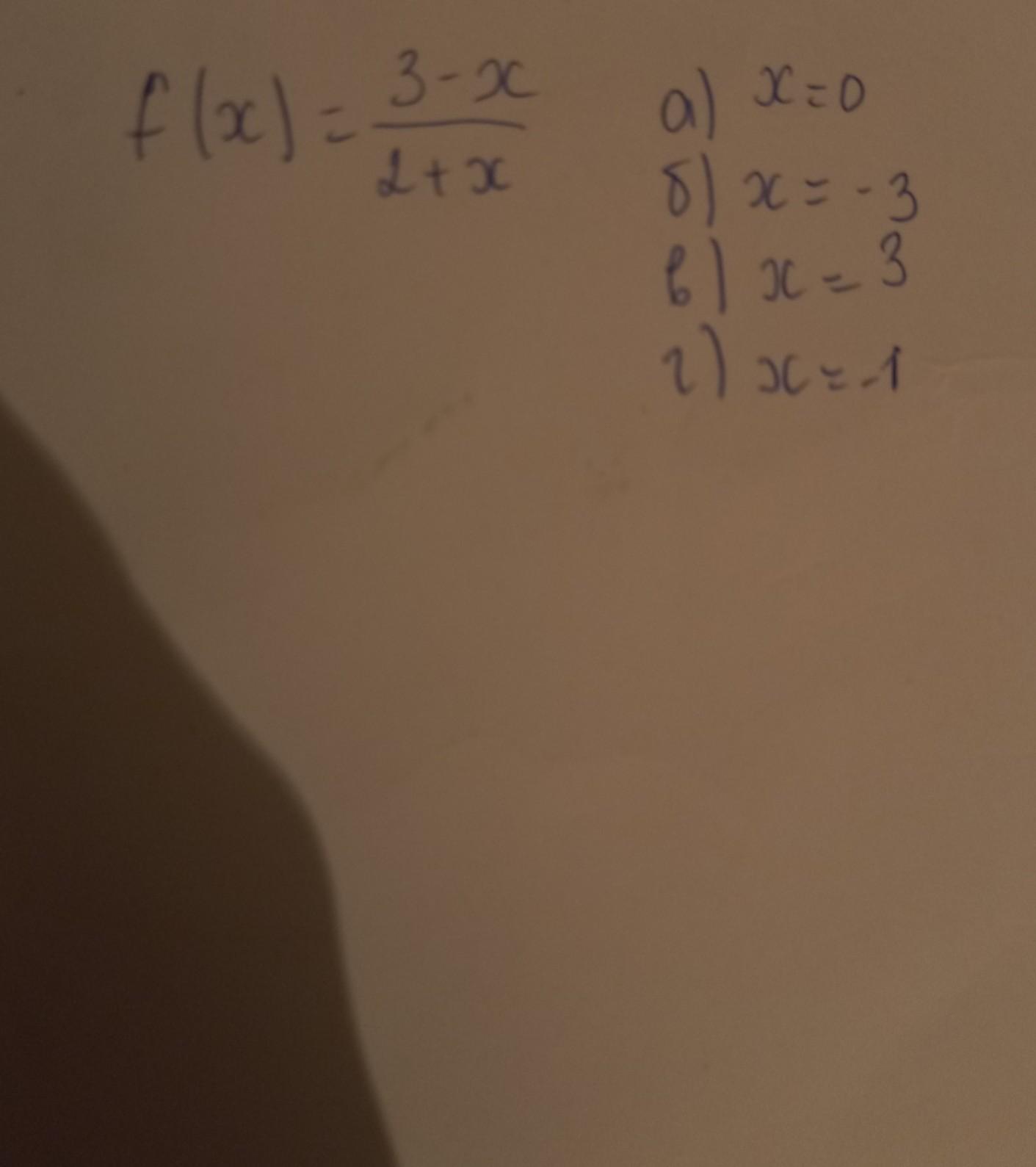
Ответы
Автор ответа:
1
Ответ:
UWU
Объяснение:
сначала найдём производную
Вот формулы, которую я буду применять , а - цифра или выражение содержащая х, b - выражение содержащее х.
(cx)'=c
(c)'=0, c - число
(x±y)'=x'±y' , ну короче стандарт
теперь подставим х
zeynepennazarova:
спасибо вам большое!
вы мне очень помогли
Похожие вопросы
Предмет: Биология,
автор: Tytyryt
Предмет: Математика,
автор: fratovcankiril
Предмет: Українська мова,
автор: polisukanna692
Предмет: Математика,
автор: Olga175t
Предмет: Русский язык,
автор: fetisovaekaterina89