Предмет: Алгебра,
автор: Lettuce13
Решите неравенство. В ответе укажите наибольшее целое решение.
Приложения:
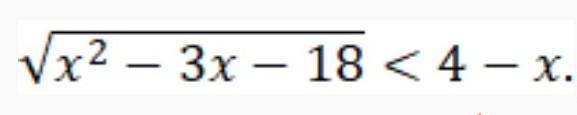
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Вспомним , что неравенство вида равносильно системе
Тем самым мы получим :
Похожие вопросы
Предмет: История,
автор: krykunlorik
Предмет: Информатика,
автор: dostaevskii8198
Предмет: Математика,
автор: vivaneviva
Предмет: Другие предметы,
автор: gulnaz1706