Предмет: Алгебра,
автор: Viscount
Решите парочку показательных неравенств.
Отдаю 25 баллов
Приложения:
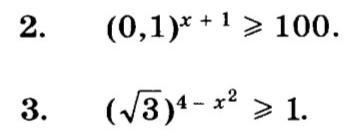
Ответы
Автор ответа:
1
2.
т.к 0 < 0,1 < 1 , знак меняется на противоположный
3.
Похожие вопросы
Предмет: Русский язык,
автор: kojcumanovnurik0
Предмет: Химия,
автор: kukukukutnyj
Предмет: Литература,
автор: ksushakriachko
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: kusajynnazym