Предмет: Геометрия,
автор: vladprodous99
Укажіть площу трикутника сторони якого
Дорівнюють 13 см, 24 см і 13 см.
Ответы
Автор ответа:
1
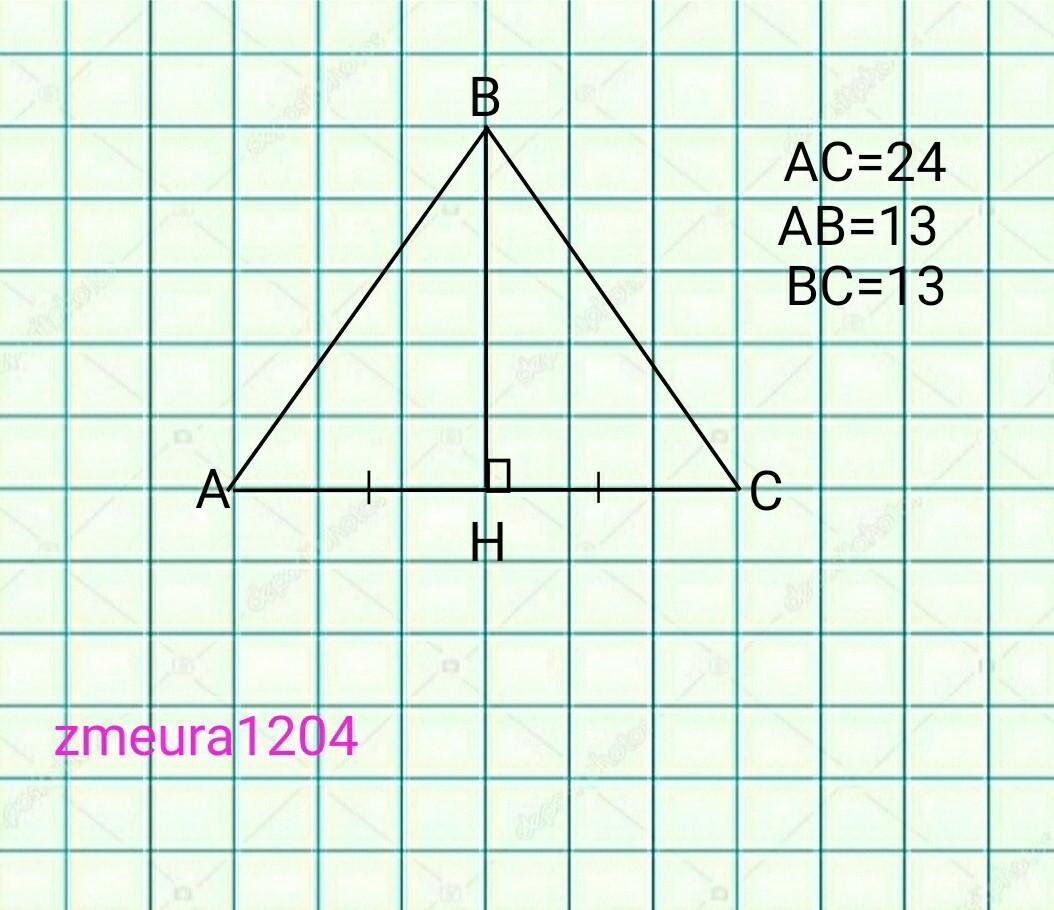
Ответ:
S(∆ABC)=60см²
Объяснение:
BH- висота, медіана і бісектриса рівнобедреного трикутника ∆АВС (АВ=ВС, за умови)
АН=НС, ВН- медіана.
АН=АС/2=24/2=12см.
∆АВН- прямокутний трикутник.
За теоремою Піфагора:
ВН=√(АВ²-АН²)=√(13²-12²)=5см.
S(∆ABC)=½*BH*AC=½*24*5=60см²
Приложения:
Автор ответа:
1
Завдання: Укажіть площу трикутника сторони якого дорівнюють 13 см, 24 см і 13 см.
Розв'язання:
Скористаємося формулою Герона:
де р - напівпериметр; а, b, c - сторони трикутника. Тоді,
Відповідь: 60 см²
Похожие вопросы
Предмет: Алгебра,
автор: bgh893971
Предмет: Українська мова,
автор: vpolak161
Предмет: Українська мова,
автор: bogdanadaniluk87
Предмет: Немецкий язык,
автор: gle89192
Предмет: Қазақ тiлi,
автор: markhelp1