Предмет: Математика,
автор: denysandrusiak
x^2+xy^3 = 192
x^3y+x^2y^2 = 96
Приложения:
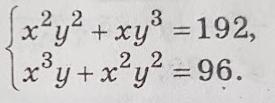
Ответы
Автор ответа:
1
Ответ:
сокращаем на общий делитель x+y;y;x и 96:
сокращаем на общий делитель x:
делим обе стороны уравнения на 6:
Похожие вопросы
Предмет: Українська література,
автор: sashavb67777
Предмет: Английский язык,
автор: rma98598
Предмет: Математика,
автор: Evelunawwl
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: nini23