Предмет: Математика,
автор: dkuznetspv
Помогите пожалуйста, высшая математика.
Приложения:
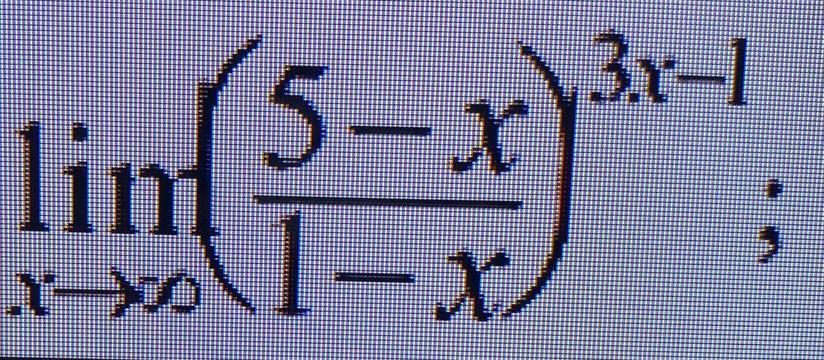
Ответы
Автор ответа:
1
Ответ:
Предел:
Примечание:
Теорема:
Пошаговое объяснение:
.
Похожие вопросы
Предмет: Математика,
автор: nlukavytsja104
Предмет: Українська мова,
автор: Osjsbxhsuosls
Предмет: Физика,
автор: gritcenkoangelina34
Предмет: История,
автор: vaseevaevgeniya81
Предмет: Қазақ тiлi,
автор: danauali