Срочно!! С подробный решением задачи!
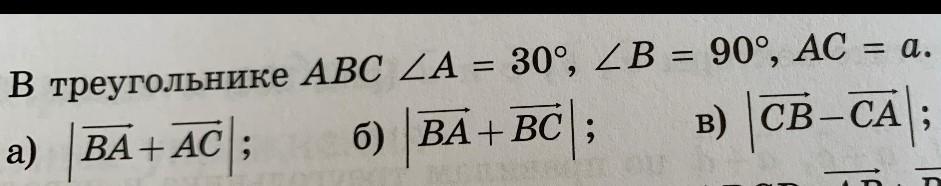
Ответы
Ответ:
Модули векторов:
а)
б)
в)
Объяснение:
Дано: ∠A = 30°, ∠B = 90°, AC = a
Найти:
Решение:
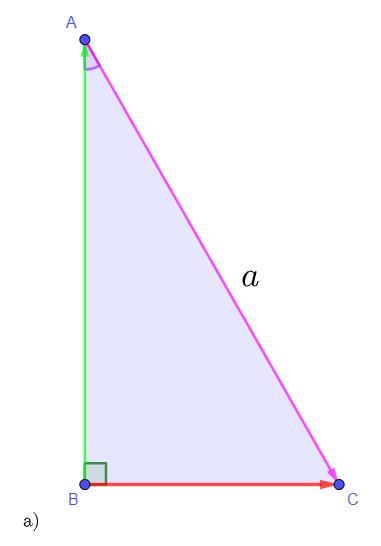
- а)
Так как по условию угол ∠B = 90°, то определению
треугольник ΔABC - прямоугольный.
По правилу треугольника для сложения векторов:
По определению синуса в прямоугольном треугольнике (ΔABC):
, таким образом:
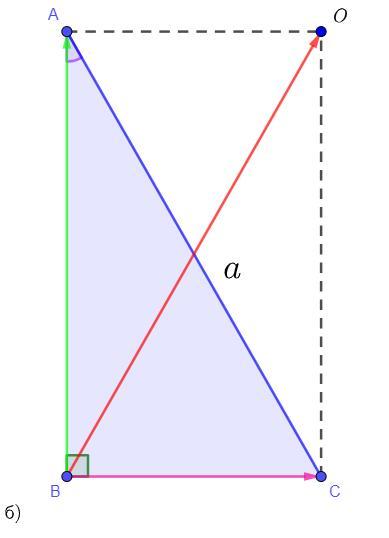
- б)
По правилу параллелограмма для сложения векторов:
Достроим треугольник ΔABC до параллелограмма таким образом, что , то есть ABCO - параллелограмм.
Так как по условию угол ∠B = 90°, то по теореме если один из углов параллелограмма равен 90°, то данный параллелограмм - прямоугольник, тогда ABCO - прямоугольник.
По свойствам прямоугольника (ABCO) его диагонали равны, тогда , таким образом
.
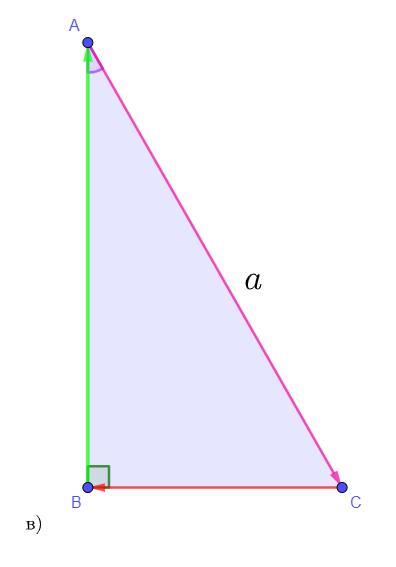
- в)
По свойствам векторов:
По определению синуса в прямоугольном треугольнике (ΔABC):
.