Предмет: Геометрия,
автор: krrristi
в равнобедренном треугольнике боковая сторона равна 44, а основание - 44. найди площадь данного треугольника.
Приложения:
zmeura1204:
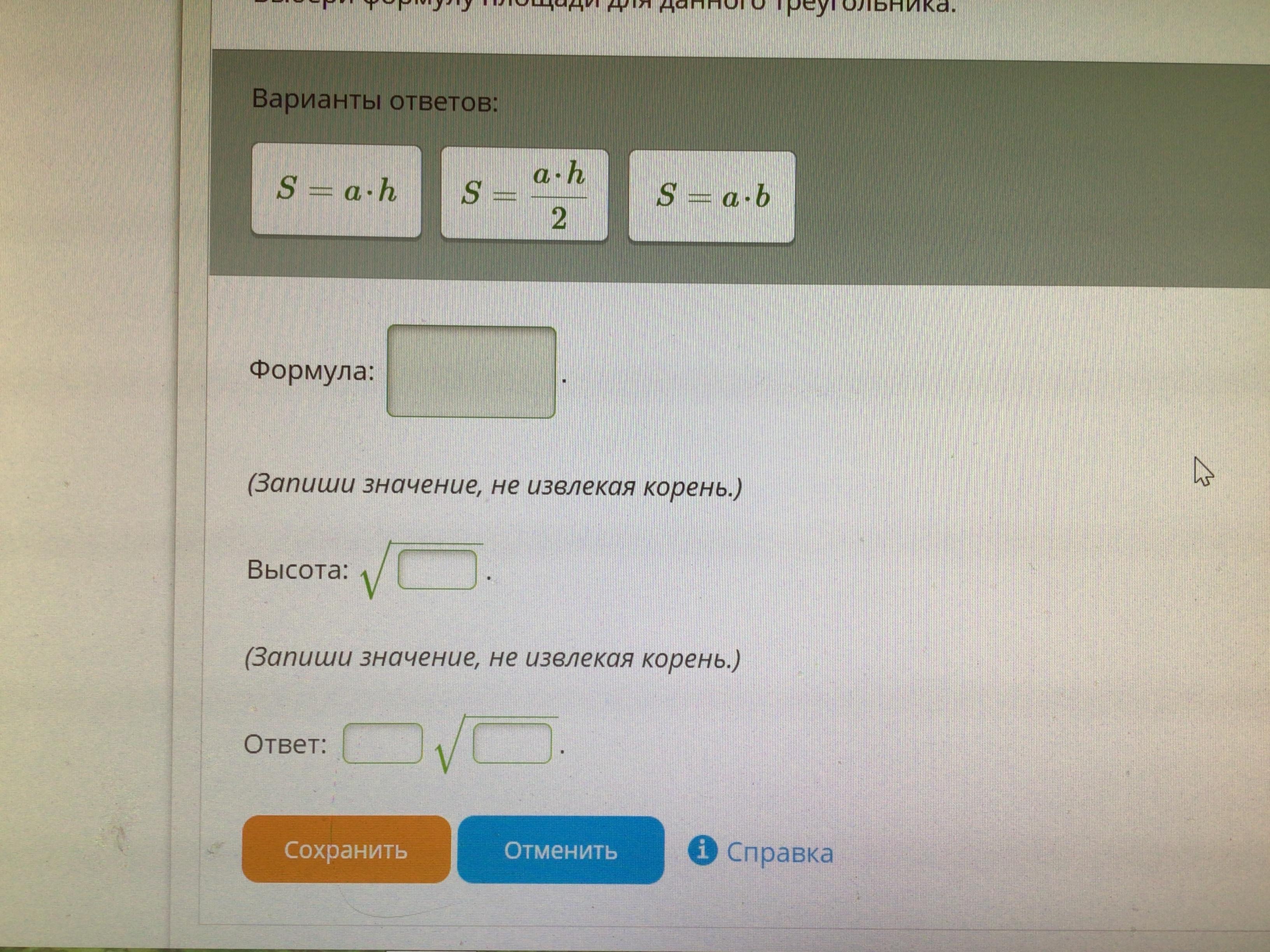
Равносторонний треугольник?
Высота 1452
Ответ: 484√3
S=ah/2
Ответы
Автор ответа:
1
Объяснение:
Если мы в этом треугольнике опустим высоту на основание, получим два прямоугольных треугольника. Т.к. в равнобедренном треугольнике высота это и медиана и биссектриса, тогда основание высотой поделится на два равных отрезка, 22 каждый.
Если в прямоугольном треугольнике мы знаем гипотенузу(боковую сторону) и катет(половина основания), можем найти второй катет(высоту).
По теореме Пифагора: высота=
Вытота получается равной
А чтобы найти площадь треугольника, нужно высоту умножить на основание и поделить все на два.
Это и есть ответ. Осталось только поделить 44 на 2.
А вообще это равносторонний треугольник и площадь можно найти по формуле
Где x-сторона треугольника.
всё правильно, кроме третьего варианта.
Похожие вопросы
Предмет: Русский язык,
автор: alinaprihodko0703
Предмет: ОБЖ,
автор: mariiaalalspal
Предмет: Алгебра,
автор: Pavelsampanov33
Предмет: Физика,
автор: Monkii