Предмет: Алгебра,
автор: Jaguar444
Решите неравенство с окружностью.
ctg(x-π/6) < √3
ctg(x+π/3) > √3/3
Подробно!
Ответы
Автор ответа:
1
Ответ:
Решить тригонометрическое неравенство .
Сделаем замену:
Приложения:
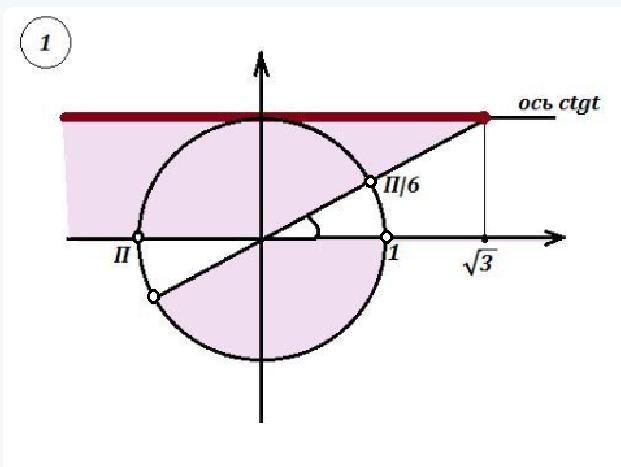
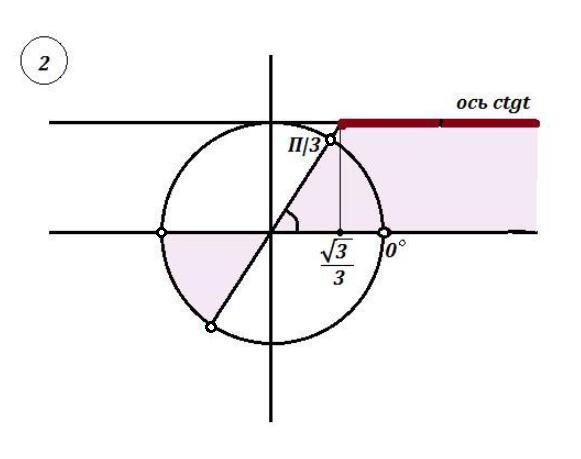
Jaguar444:
Спасибо большое!
здравствуйте, помогите пожалуйста с алгеброй, отмечу как лучший ответ и 5 звёзд
https://znanija.com/task/51059782?utm_source=android&utm_medium=share&utm_campaign=question
https://znanija.com/task/51059782?utm_source=android&utm_medium=share&utm_campaign=question
Похожие вопросы
Предмет: Математика,
автор: mahmudovemil229
Предмет: Другие предметы,
автор: jokervalerian
Предмет: Қазақ тiлi,
автор: 011119sof
Предмет: Химия,
автор: lskandar