Предмет: Алгебра,
автор: person4884
Можете,пожалуйста, помочь. С объяснением! Кстати, в каких случаях ОДЗ надо писать, а в каких не надо?
Приложения:
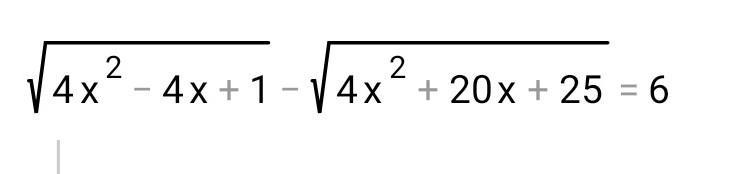
Simba2017:
одз здесь нашли?
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Заметим , что под корнем представлены полные квадраты :
ОДЗ здесь не нужно , главное вспомнить что
* √a² = |a|
И таким образом , мы получим модульное уравнение :
— — + 2x - 1
— + + 2x + 5
Это означает , что уравнение имеет бесконечное множество решений когда x ∈ ( -∞ ; -2,5 )
Объединив решения мы получим :
Спасибо. Не могли бы Вы подсказать, в каких случаях мне придеться писать ОДЗ
ОДЗ нужно писать только когда у корня радикал четной степени , таким образом подкоренное выражение должно быть больше нуля или равно нулю , но в данном случае для одз немного другое правило √(a²) = |a| , т.к мы сначала возводим наше выражение в квадрат . Но , а если было бы наоборот , т.е мы сначала вязли корень , а потом возвели бы в квадрат , тут действовало бы одз (√a )² , a > 0 или a = 0
понятно. Большое спасибо! =)
Похожие вопросы
Предмет: Алгебра,
автор: nasters
Предмет: Алгебра,
автор: suvorintimur2010
Предмет: Алгебра,
автор: 067280
Предмет: Русский язык,
автор: vloganastazy
Предмет: История,
автор: ocheretyanniyyarosla