Question

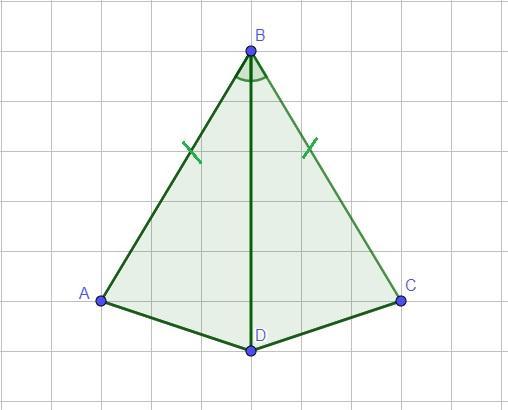
ВД – бісектриса кута АВС. АВ = СВ. За якою ознакою рівні трикутники АВД і СВД?

Answer 1

Ответ:

ΔABD=ΔCBD за першою ознакою.

Объяснение:

ВD – бісектриса кута АВС. АВ = СВ. За якою ознакою рівні трикутники АВD і СВD?

Перша ознака рівності трикутників (за двома сторонами і кутом між ними):

• Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники є рівними.

Розв'язання

Розглянемо ΔАВD і ΔСВD. У них:

• так як ВD – бісектриса ∠АВС, то ∠АВD=∠CBD (за означенням бісектриси кута)
• АВ = СВ за умовою
• BD - спільна

Тому ΔАВD = ΔСВD за І ознакою (за двома сторонами і кутом між ними)

#SPJ1