Предмет: Алгебра,
автор: kabinkasabinka
Помогите пожалуйста!!
Приложения:
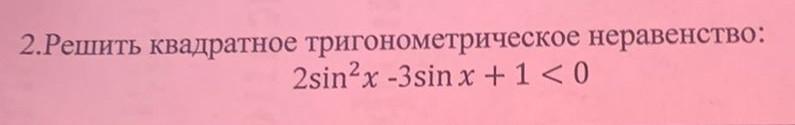
Ответы
Автор ответа:
1
Ответ:
x∈(π/6+2πn ; π/2+2πn)U(π/2+2πn ; 5π+2πn) , где n - целое число
Объяснение:
2.Решите квадратное тригонометрическое неравенство: 2sin²x - 3sinx + 1 < 0
Заменим sinx = t , где t∈[-1;1] , тогда :
Найдём нули:
Следовательно , 1/2 < t < 1 , вернемся к старой замене :
Тогда, получим совокупность неравенств:
Объеденив всё это, придём к тому , что:
x∈(π/6+2πn ; π/2+2πn)U(π/2+2πn ; 5π/6+2πn) , где n - целое число
Приложения:

Похожие вопросы
Предмет: Математика,
автор: 3inkonastya
Предмет: Математика,
автор: kirakarakulova2
Предмет: Українська література,
автор: germanteposer
Предмет: Английский язык,
автор: dmekvabishvili
Предмет: Математика,
автор: indikot51