Предмет: Алгебра,
автор: lmgpgepnpg
Спростіть вираз
(a-b)(a+b)(a²+ b²)(a⁴+ b⁴)(a(8в степені) ) + b(8в степені) )•(a(16 в степені) + b(16в степені) )
Приложения:
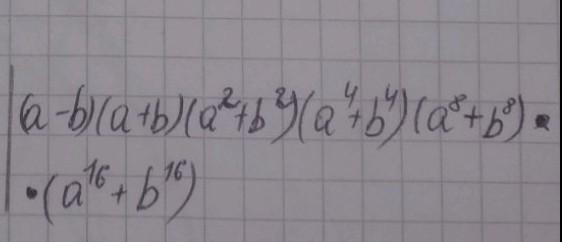
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Формула для решения - разность квадратов:
Автор ответа:
0
Ответ:
Объяснение:
Это задача на многократное использование формулы
Похожие вопросы
Предмет: Физика,
автор: ddasha0926
Предмет: Другие предметы,
автор: ddffggfgfgfgfg
Предмет: Химия,
автор: betty04010754
Предмет: Алгебра,
автор: leralashinska
Предмет: Математика,
автор: oksanagm81