Question

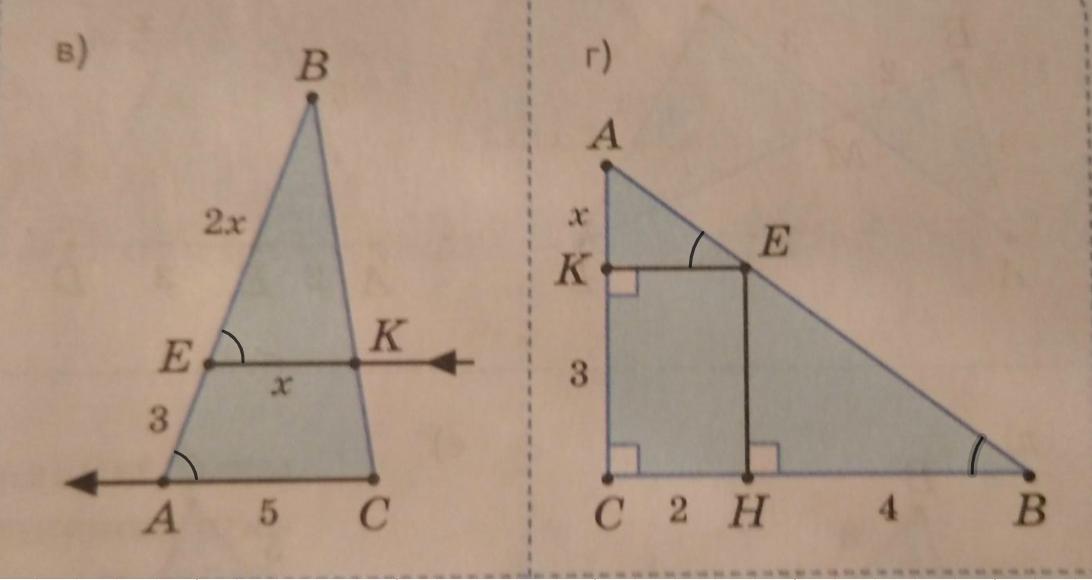
Укажите подобные треугольники на рисунке 27, а-м и найдите длину отрезка, обозначенную на каждом из рисунков буквой х. На рисунках в пунктах a, в, u , к стрелками указаны параллельные прямые, а в пунктах д, е, ж, з, и изображенный четырехугольник ABCD является параллелограммом.​

Answer 1

Ответ:

a) ΔЕВК ~ ΔАВС; ЕК = 7; ВЕ = 14.

г) ΔКАЕ ~ ΔСАВ; ΔНЕВ ~ ΔСАВ; ΔКАЕ ~ ΔНЕВ; AK = 1,5

Объяснение:

Укажите подобные треугольники на рисунке 27, а-м и найдите длину отрезка, обозначенную на каждом из рисунков буквой х. На рисунках в пунктах a, в, u , к стрелками указаны параллельные прямые.

а) Дано: ΔАВС;

ЕК || АС;

ВЕ = 2х; АЕ = 3; ЕК = х; АС = 5.

Найти: ВЕ и ЕК

Решение:

Рассмотрим ΔЕВК и ΔАВС.

ЕК || АС (условие)

• При пересечении двух параллельных прямых секущей соответственные углы равны.

⇒ ∠ВЕК = ∠ВАС (соответственные при ЕК || АС и секущей АВ)

∠В - общий

ΔЕВК ~ ΔАВС (по двум углам)

Запишем отношения сходственных сторон:

$\displaystyle \frac{EK}{AC}=\frac{BE}{BA} \\\\\frac{x}{5}=\frac{2x}{2x+3} \\\\5\cdot 2x=x\cdot (2x+3)\\\\10x=2x^2+3x\\\\2x^2-7x=0\\\\x(x-7)=0\\\\x_1=0;\;\;\;\;\;x=7$

х₁ не подходит по условию задачи.

ЕК = 7; ВЕ = 14.

г) Дано: ΔАВС - прямоугольный;

ЕК ⊥ АС; ЕН ⊥ СВ;

АК = х; КС = 3; СН = 2; НВ = 4

Найти: АК

Решение:

ЕК ⊥ АС; ВС ⊥ АС.

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ КЕ || CB

ЕН ⊥ ВС; АС ⊥ ВС  ⇒ АС || ЕН

⇒ СКЕН - параллелограмм.

Стороны перпендикулярны ⇒ СКЕН - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ СН = КЕ = 2.

Рассмотрим ΔКАЕ и ΔСАВ - прямоугольные.

∠КЕА = ∠В (соответственные при КЕ || CB и секущей АВ)

ΔКАЕ ~ ΔСАВ (по двум углам)

Напишем отношения сходственных сторон:

$\displaystyle \frac{KE}{CB}=\frac{AK}{AC} \\\\\frac{2}{2+4}= \frac{x}{x+3}\\ \\6\cdot x=2\cdot(x+3)\\\\6x=2x+6\\\\4x=6\\\\x=1,5$

AK = 1,5

Найдем еще подобные треугольники.

Рассмотрим ΔНЕВ и ΔСАВ - прямоугольные.

∠В - общий.

⇒ ΔНЕВ ~ ΔСАВ (по двум углам).

Рассмотрим ΔКАЕ и ΔНЕВ - прямоугольные.

∠КЕА = ∠В

⇒ ΔКАЕ ~ ΔНЕВ (по двум углам)

#SPJ1