Question

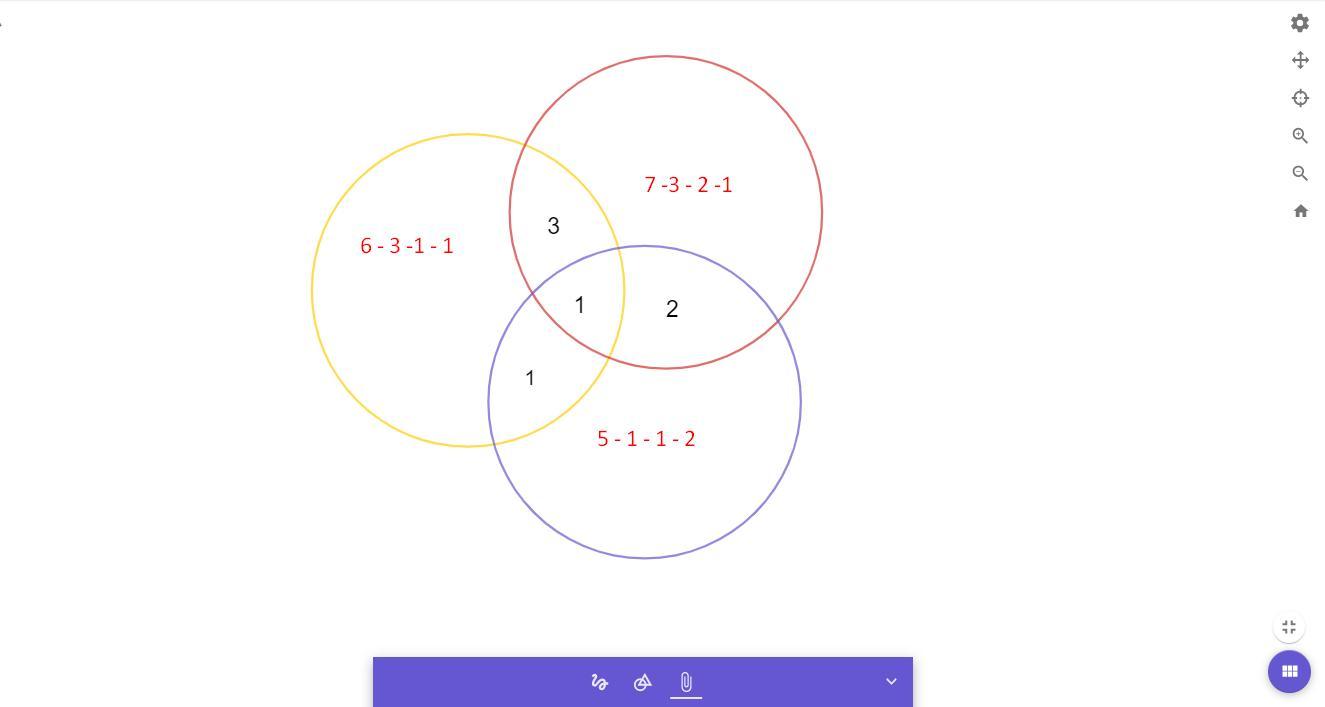
Реши задачу с помощью кругов Эйлера.
В многодетной семье дети любят фрукты. Яблоки любят 7 де-
тей, абрикосы – 6 детей, виноград – 5, яблоки и абрикосы – 4,
яблоки и виноград – 3, абрикосы и виноград – 2. И только один
любит абрикосы, яблоки и виноград. Сколько детей в семье?

Answer 1

Ответ: В семье всего 10 детей .

Пошаговое объяснение:

Определимся , что :

Красный круг   - яблоки

Желтый  круг  - абрикосы  

Фиолетовый  круг  - виноград

Теперь отображаем на диаграмме :

1 - ребенок любит все фрукты ,  т.е  он является общим пересечением для всех трех кругов

Найдем кол-во детей которые  любят  и  яблоки и абрикосы , отнимаем от их кол-ва  ребенка который любит все фрукты  

4 - 1 = 3  (пересечение  только  для красного и желтого круга)

И аналогично , находим тех кто любит только любит  и яблоки и виноград :

3 - 1 = 2   (пересечение только  для красного и фиолетового круга)

Абрикосы и виноград :

2 - 1 = 1  (пересечение только  для желтого  и фиолетового круга)

Теперь , найдем детей которые любят исключительно один фрукт

(т.е  которые предпочитают только один из фруктов )

Учтем в каждом круге общее число людей которые любят определенный фрукт , т.е

Красный круг  -  7

Желтый  круга  - 6

Фиолетовый - 5

Таким образом :

Только яблоки любит   7 - 1 - 2 - 3 = 1 ч

Только  абрикосы    любит  6 - 3 - 1 - 1 = 1 ч

Только виноград любит  5 - 2 - 1  - 1 = 1 ч   (рис1)

По итогу складываем все числа которые есть  на диаграмме (рис2)

1 + 1 + 1 + 3 +1 + 2 + 1  = 6 + 4 = 10

#SPJ1