Question

ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО СДЕЛАЙТЕ ПОЛНОСТЬЮ ВСЕ ЗАДАНИЕ

Answer 1

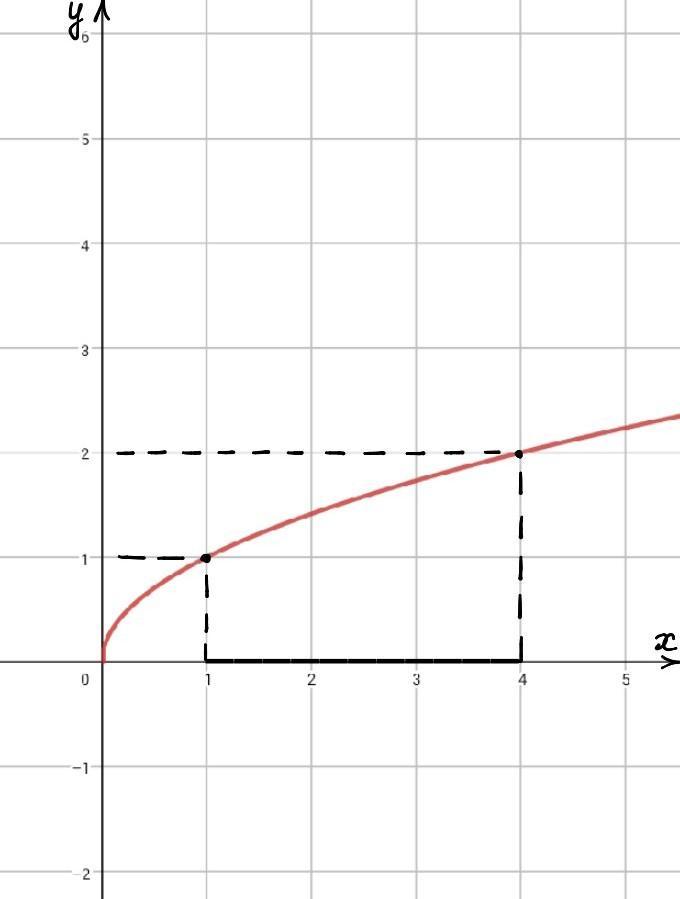
Найти наибольшее и наименьшее значение функции y = x^½ на отрезке [1;4].

⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

$\displaystyle y = x^{\frac{1}{2}}$

• Воспользуемся одним из свойств степеней: $\displaystyle \tt \sqrt[a]{b^k} = b^{\frac{k}{a}},\,k \in Z,\, a \ne0$

$\displaystyle \boldsymbol{y = \sqrt{x} }$

• Функция является возрастающей, область ее определения D(y) = [0;+∞). Т.к. концы включенные, то просто нужно их подставить в нашу формулу.

у(1) = √1 = 1

у(4) = √4 = 2.

Ответ: $\displaystyle \boldsymbol{y_{max}= 2,\, y_{min}= 1}$

Answer 2

Ответ:

$y_{min} = 1 \\ y_{max} = 2$

Объяснение:

1 способ(для рассуждения)

$y = x {}^{ \frac{1}{2} }$

Можно записать как: $y = \sqrt{x}$

Очевидно , что x∈[0;+∞) , график данной функции постоянно возрастает , а это значит , что если взять любой отрезок из оси Ох , то только при концах этого отрезка функция будет иметь наименьшее и наибольшее значение.

Наш отрезок [1;4] , найдем наименьшее и наибольшее значение функции:

$y(1) = \sqrt{1} = 1 \\ y(4) = \sqrt{4} = 2$

Следовательно , наименьшее это 1 , а наибольшее это 2

2 способ

Надём производную функции $y = \sqrt{x}$:

Согласно производной корня : $\bf (\sqrt{x})'=\frac{1}{2\sqrt{x}}$

$\displaystyle y'=\frac{1}{2\sqrt{x}}$

Найдём нули производной y'(x)=0:

$\displaystyle \frac{1}{2\sqrt{x}}=0\\x\in \varnothing$

Нулей производной функция не имеет. Значит , минимальное и максимальное значение функция имеет при концах отрезка , то есть:

$\displaystyle y(1)=\sqrt{1}=1\\ y(4)=\sqrt{4}=2$