Предмет: Алгебра,
автор: aruzhankerimkul03
int dx sqrt(5x ^ 2 + 3) как решать?
Приложения:
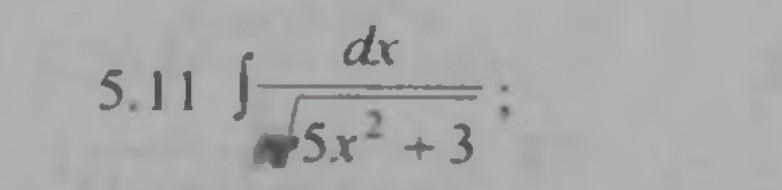
Ответы
Автор ответа:
0
Ответ:
Интеграл:
Примечание:
По таблице производных:
По свойствам интегралов:
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: mashadacenko745
Предмет: Алгебра,
автор: Simbachca
Предмет: География,
автор: ryufytf
Предмет: Математика,
автор: GazyYT