Предмет: Математика,
автор: slwmlm
помогите, пожалуйста!! срочно надо
Приложения:
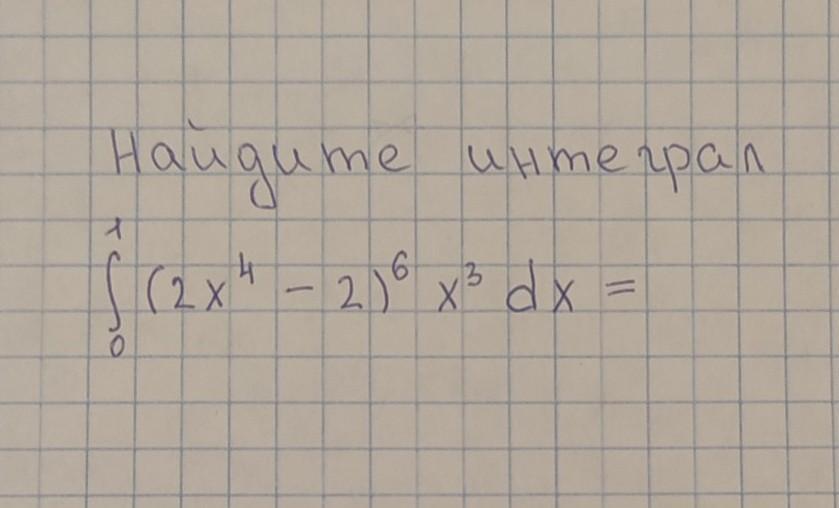
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Найти интеграл:
Заменим переменную:
Поменяем пределы интегрирования:
х = 0 ⇒ t = -2
x = 1 ⇒ t = 0
Получим интеграл:
Похожие вопросы
Предмет: Химия,
автор: ggffggff68
Предмет: Право,
автор: anatolii24663
Предмет: Английский язык,
автор: eldosbekp
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: lianakryhkova2007