Предмет: Алгебра,
автор: anakosanenko19
No5 (4 балла) Найдите область определения функции:


Найдите область значений функции на отрезке

Приложения:
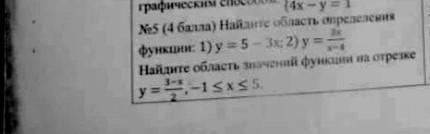
Ответы
Автор ответа:
0
Знаменатель дроби не должен равняться нулю , так как на ноль делить нельзя .
Похожие вопросы
Предмет: География,
автор: egorshavlak4
Предмет: Математика,
автор: artembekaev777
Предмет: Литература,
автор: g5s4pvjx5k
Предмет: Алгебра,
автор: Kibernet123