Трапеція. Вписані та центральні кути.
вписані та описані чотирикутники. Допоможіть з самостійною будь ласка
Ответы
Объяснение:
1.
в трапеции суммы углов прилежащих к боковой стороне равна 180:
180-50=130° третий угол
180-120=60° четвёртый угол
2.
окружность можно вписать в четырехугольник,если суммы противоположных сторон равны.
5х одна сторона
2х вторая сторона
х третья сторона
4х четвертая сторона
5х+х=2х+4х
6х=6х верно
можно вписать.
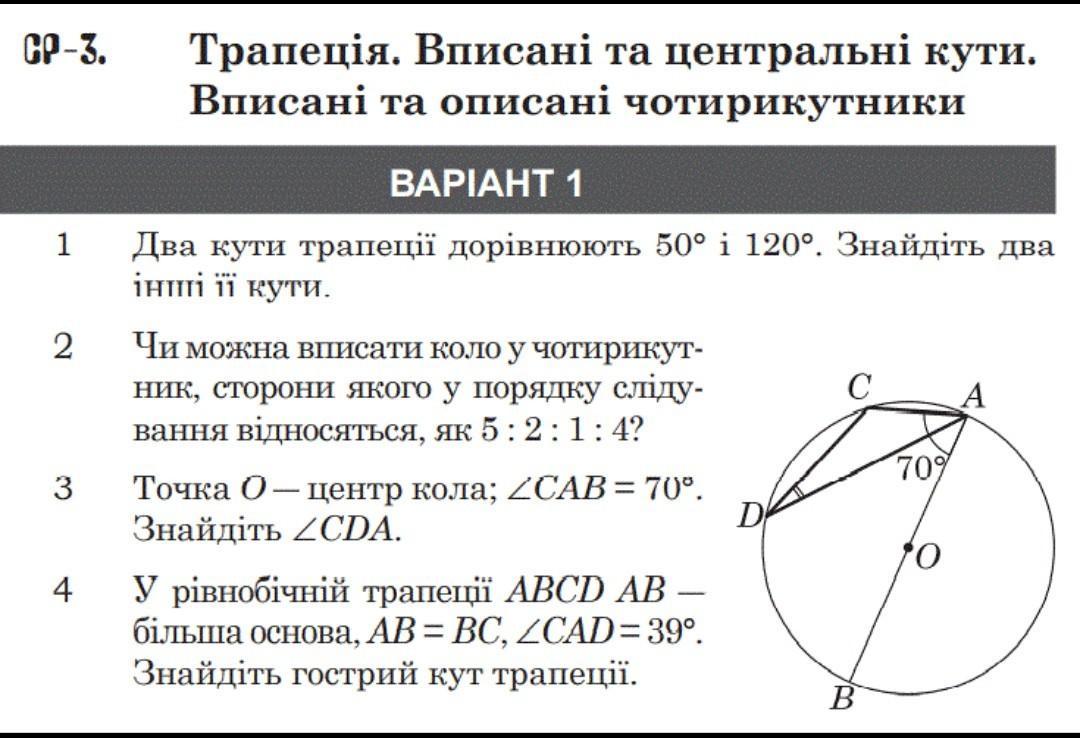
3.
вписанный угол равен половине дуги на которую опирается.
⋃CDB=2•∠CAB=2•70=140°
⋃АС=180-⋃СDB=180-140=40°
∠СDA=⋃AC:2=40:2=20°
4.
АВСD -равнобедреная трапеция
АВ - большее основание
∠CAD=39°
АВ=ВС
Найти: ∠DAB =∠ABC
Если АВ=ВС ,то диагональ АС - биссектриса,т.к
отсекает равнобедренный треугольник АВС.
Пусть ∠САВ=∠АСВ=х°,тогда ∠DAB=39+x°.
∠АВС=∠DAB=39+x°.
Сумма углов ∆АВС=180°:
2∠САВ+∠АВС=180
2х+39+х=180
3х=180-39
3х=141
х=47°
∠САВ=∠АСВ=47°
∠DAB=∠ABC=39+47=86°
ответ: 86°
ответ: