Предмет: Алгебра,
автор: sangers655
помогите пожалуйста решить задачу Коши
Приложения:
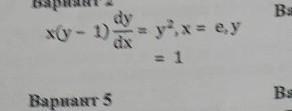
Ответы
Автор ответа:
1
Ответ:
Частный интеграл:
Подставим начальные условия и найдём значение С .
Частный интеграл: .
Похожие вопросы
Предмет: Литература,
автор: lerakolodko534
Предмет: Математика,
автор: lomimiks
Предмет: Английский язык,
автор: parshina43
Предмет: Математика,
автор: mixam79
Предмет: Математика,
автор: Аноним