Предмет: Математика,
автор: Gansta2281
найдите значение производной функции f(x)=

в точке x0=2 (на фото подробнее)
Приложения:
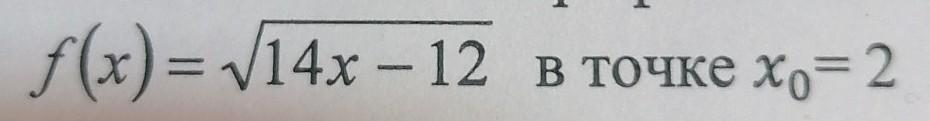
Ответы
Автор ответа:
2
Решение:
Формулы для решения:
Ответ: 1,75
Gansta2281:
по-моему все решение не влезло
Сможете отправить полное куда-нибудь?
Здесь представлено полное решение.
с мобильной версии отображено не всеь ответ, зашел с компьютера и увидел, спасибо большое
Похожие вопросы
Предмет: Английский язык,
автор: fcuheuk205
Предмет: Українська мова,
автор: hludbogdan2011
Предмет: География,
автор: resuldurdygulyyew777
Предмет: Биология,
автор: aaaaaaaaa1460
Предмет: Биология,
автор: derbas2816