Предмет: Геометрия,
автор: sevaanhelis
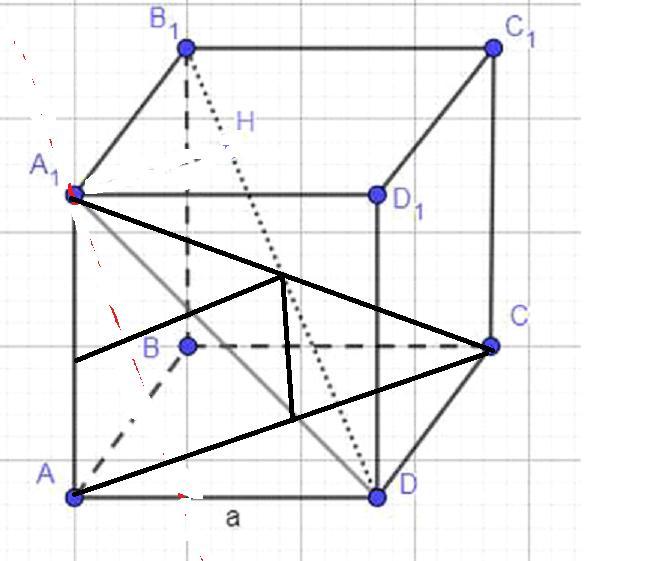
Ребро куба дорівнює a. Знайти відстань від діагоналі куба до
ребра, яке її не перетинає
Ответы
Автор ответа:
0
Через диагональ проводим плоскость0 параллельную диагонали.
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA
= 0
Подставим данные и упростим выражение:
x - 0 y - 1 z - 0
0 - 0 1 - 1 1 - 0
1 - 0 0 - 1 0 - 0
= 0
x - 0 y - 1 z - 0
0 0 1
1 -1 0
= 0
x - 0
0·0-1·(-1)
-
y - 1
0·0-1·1
+
z - 0
0·(-1)-0·1
= 0
1
x - 0
+ 1
y - 1
+ 0
z - 0
= 0
x + y - 1 = 0
Расстояние от точки до плоскости определяется по формуле:
\[ l = \frac{|a\cdot x_0+b\cdot y_0+c\cdot z_0 + d|}{\sqrt{a^2+b^2+c^2}}, \] ( подробнее во вкладке).
Подставив данные, получаем:
Расстояние равно √2/2 ≈ 0,707106781.
Графически видно, что это расстояние равно половине диагонали основания.
Приложения:

Похожие вопросы
Предмет: География,
автор: sofiyafediaieva
Предмет: Английский язык,
автор: mazurvalik56
Предмет: Математика,
автор: ermekovduit
Предмет: Экономика,
автор: ajlanakakimova
Предмет: Математика,
автор: nellibabakehan5