Предмет: Алгебра,
автор: selfcare39
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО! Сделайте полностью все задания!
Приложения:
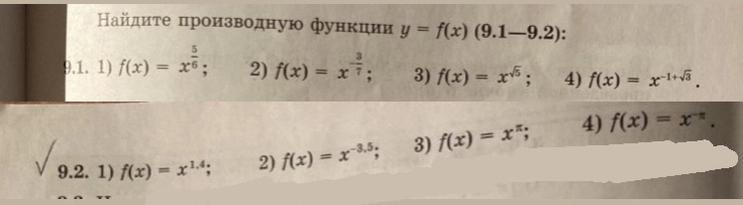
Ответы
Автор ответа:
2
Ответ:
Производная степенной функции равна .
spamgg002:
пожалуйста помогите в профиле там задание
Похожие вопросы
Предмет: Українська література,
автор: grigoalina09
Предмет: Алгебра,
автор: andriivoronov
Предмет: Математика,
автор: mazikop228
Предмет: Математика,
автор: daurenbergenovtop
Предмет: Қазақ тiлi,
автор: marinak1984