Question

5) cos2x+5cosx+3≥0
cos²x-(1-cos²x)+5cosx+3≥0
cos²x-1+cos²x+5cosx+3≥0
2cos²x+5cosx+2≥0
Пусть cosx=t , где t∈[-1;1]
2t²+5t+2≥0
Дальше дискриминант получился 9 и корни этого уравнения -2 и - 1/2 , теперь к делу , нужно мне объяснить подробно , что делать дальше?

6) Также , помогите решить это с подробным объяснением : 0<cosx≤√2/2​

Answer 1

5)

$\cos2x+5\cos x+3\geqslant0$

$2\cos^2x+5\cos x+2\geqslant 0$

Замена: $\cos x=t,\ t\in[-1;\ 1]$

$2t^2+5t+2\geqslant 0$

$2t^2+5t+2=0$

$t_1=-2;\ t_2=-\dfrac{1}{2}$

Собственно, дальше. Дальше дорешиваем неравенство методом интервалов относительно t:

$t\in(-\infty;-2]\cup\left[-\dfrac{1}{2} ;\ +\infty\right)$

Это решение можно переписать в виде совокупности, одновременно выполнив обратную замену:

$\left[\begin{array}{l} \cos x\leqslant -2 \\ \cos x\geqslant -\dfrac{1}{2} \end{array}\right.$

Поскольку косинус принимает свои значения из отрезка от -1 до 1, то первое неравенство не имеет решений.

Остается неравенство:

$\cos x\geqslant -\dfrac{1}{2}$

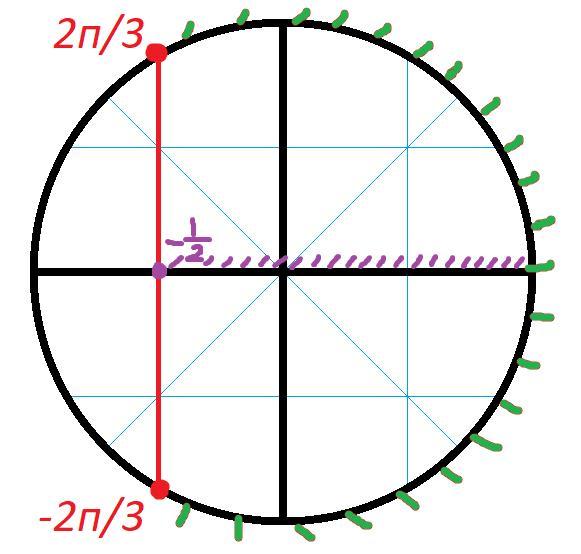
Решить его удобнее всего на окружности.

Отметим на оси х, которая соответствует значениям косинуса, точку -1/2 (фиолетовая точка). По условию, нас интересуют значения косинуса, большие или равные -1/2 (фиолетовый отрезок). Найдем дугу, которая соответствует этим значениям косинуса (зеленая дуга).

На окружности есть две точки, в которых косинус равен -1/2 (красные точки). Учитывая знак неравенства, запишем:

$-\dfrac{2\pi }{3} \leqslant x\leqslant \dfrac{2\pi }{3}$

Говоря точнее, точек было не две, а две серии (графически, это по-прежнему две точки). Учитывая периодичность косинуса следует записать:

$\boxed{-\dfrac{2\pi }{3}+2\pi n \leqslant x\leqslant \dfrac{2\pi }{3}+2\pi n,\ n\in\mathbb{Z}}$

6)

$0 < \cos x\leqslant \dfrac{\sqrt{2} }{2}$

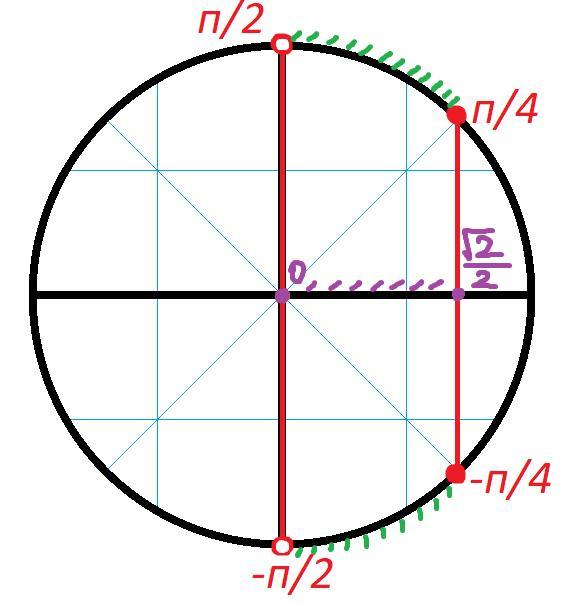
Вновь ищем решение на окружности.

Отметим на оси х точки 0 и $\dfrac{\sqrt{2}} {2}$. Нас интересуют значения косинуса, большие 0, но меньшие или равные $\dfrac{\sqrt{2}} {2}$. Найдем, какие дуги соответствуют этому условию.

На окружности есть две серии точек, в которых косинус равен 0, и две серии точек, в которых косинус равен $\dfrac{\sqrt{2}} {2}$.

Записываем решение:

$\boxed{x\in\left(-\dfrac{\pi}{2} +2\pi n;\ -\dfrac{\pi }{4} +2\pi n\right]\cup\left[\dfrac{\pi }{4} +2\pi n;\ \dfrac{\pi}{2} +2\pi n\right),\ n\in\mathbb{Z}}$