Предмет: Алгебра,
автор: 01maksymko10
Розв'яжіть нерівність log^2 1/4 X + log1/4 X-2>=0
Приложения:
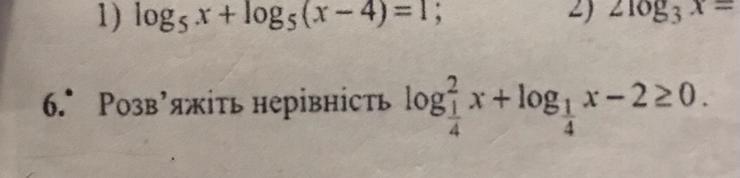
Ответы
Автор ответа:
0
Ответ:
Решим квадратное неравенство относительно функции .
Сделаем замену .
Вернёмся к старой переменной .
Функция убывающая, поэтому
Ответ: .
Похожие вопросы
Предмет: Физика,
автор: dashamiseyuk07
Предмет: Английский язык,
автор: ksenialitvinenko786
Предмет: История,
автор: d8309344
Предмет: Алгебра,
автор: VredyWey
Предмет: Геометрия,
автор: nikita711718