Question

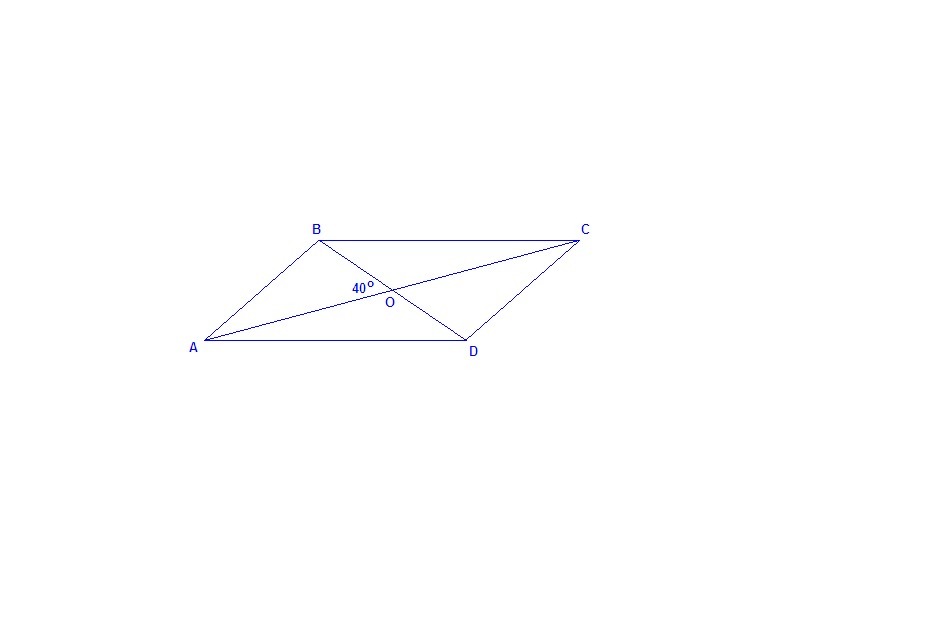
Найдите стороны параллелограмма, если его диагонали равны 40см и 24см, а угол между диагоналями равен 40 граудсов.

Answer 1

Диагонали параллелограмма точкой пересечения делятся пополам, ⇒

АО = ОС = АС / 2 = 20 см

BO = OD = BD /2 = 12 см

Из ΔАВО по теореме косинусов:

АВ² = АО² + ВО² - 2АО·ВО·cos40°

AB² ≈ 400 + 144 - 2 · 20 · 12 · 0,766 ≈ 176,32

AB ≈ 13,3 см

∠ВОС = 180° - 40° = 140° (смежные)

Из треугольника ВОС по теореме косинусов:

BC² = BO² + CO² - 2BO·CO·cos140°

BC² ≈= 144 + 400 - 2 · 12 · 20 · (- 0,766) ≈ 911,68

BC ≈ 30,2 см

Противоположные стороны параллелограмма равны.

AD = BC ≈ 30,2 см

AB = CD ≈ 13,3 см