Question

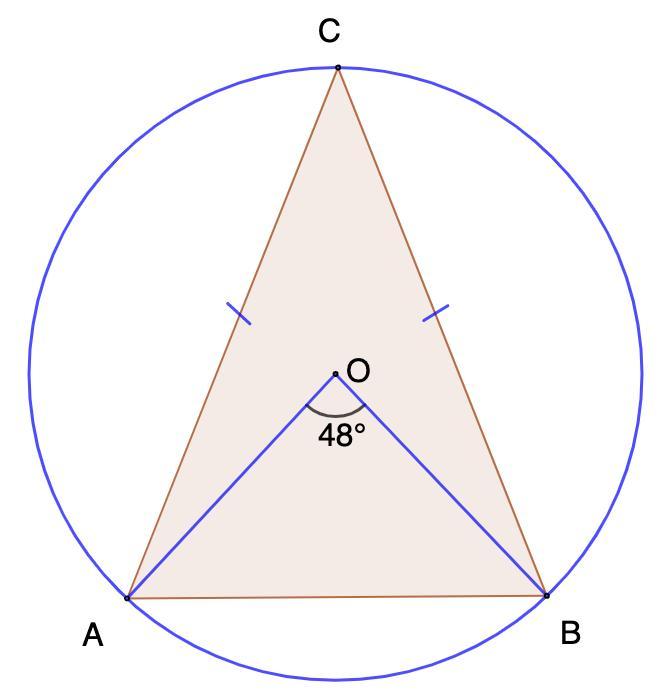
точка O центр кола, описаного навколо рівнобедреного трикутника A, B, C (AC=BC). Знайдіть кути трикутника ABC якщо кут AOB=48°​

Answer 1

Ответ:

Углы треугольника равны: ∠А = ∠В = 78°; ∠С = 24°.

Объяснение:

Точка О - центр окружности, описанной вокруг равнобедренного треугольника ABC (AC = BC). Найдите углы треугольника ABC если угол AOB = 48°​.

Дано: ΔАВС - равнобедренный (AC = BC);

Окр.О - описана около ΔАВС;

∠AOB = 48°​.

Найти: ∠А; ∠В; ∠С.

Решение:

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠АОВ = ◡АВ = 48° (центральный)

• Вписанный угол равен половине градусной меры дуги, на которую он опирается.

⇒ ∠С = ◡АВ : 2 = 48° : 2 = 24° (вписанный)

• Сумма углов треугольника равна 180°.

⇒ ∠А + ∠В = 180° - ∠С = 180° - 24° = 156°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠А = ∠В = 156° : 2 = 78°

Углы треугольника равны: ∠А = ∠В = 78°; ∠С = 24°.

#SPJ1