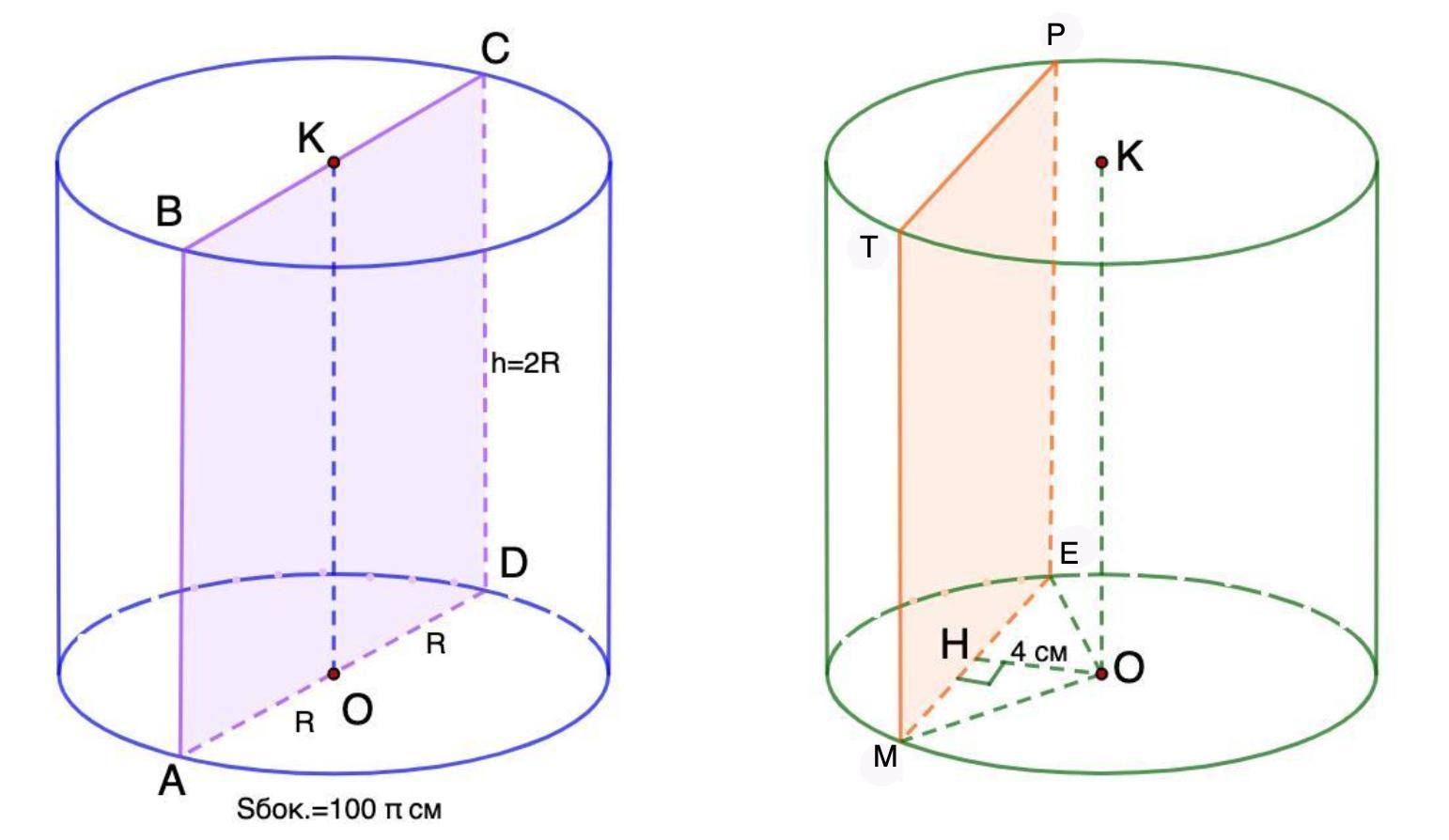
Висота циліндра вдвічі більша за його радіус. Площа бічної поверхні
циліндра дорівнює 100п см². 1)Знайдіть площу осьового перерізу циліндра:
2) Знайдіть площу перерізу циліндра, побудованого паралельно його осі на відстані 4 см від неї
з малюнком
Ответы
Ответ:
Площадь осевого сечения цилиндра равна 100 см².
Площадь сечения цилиндра, построенного параллельно его оси на расстоянии 4 см от нее, равна 60 см².
Объяснение:
Высота цилиндра вдвое больше его радиуса. Площадь боковой поверхности цилиндра равна 100π см².
1) Найдите площадь осевого сечения цилиндра;
2) Найдите площадь сечения цилиндра, построенного параллельно его оси на расстоянии 4 см от нее.
Дано: цилиндр;
Sбок = 100π см²;
h = 2R см;
ABCD - осевое сечение;
МРТЕ || KO,
OH = 4 см.
Найти: S(ABCD); S(MTPE).
Решение:
1) Рассмотрим ABCD.
АВ = h = 2R (условие)
AD = d (диаметр) = 2R
⇒ ABCD - квадрат.
- Площадь квадрата равен квадрату его стороны.
S(ABCD) = (2R)² = 4R²
Найдем R.
Площадь боковой поверхности цилиндра равна:
- Sбок. = 2πRh
100π = 2πR·2R
100 = 4R²
R=5 (см)
Найдем площадь ABCD:
S(ABCD) = 4R²= 4 · 25 = 100 (см²)
Площадь осевого сечения цилиндра равна 100 см².
2) МТРЕ - прямоугольник.
Площадь прямоугольника равна произведению смежных сторон.
S(МТРЕ) = МЕ · h; h = 2R
Найдем МЕ.
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ ОН ⊥ МЕ
Рассмотрим ΔМЕО - равнобедренный (ОМ = ОЕ = R)
OH - высота.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒ МН = НЕ.
Рассмотрим ΔМНО - прямоугольный.
По теореме Пифагора найдем МН:
МН² = МО² - НО² = 25 - 16 = 9
МН = √9 = 3 (см)
⇒ МЕ = 6 см.
S(МТРЕ) = МЕ · h = 6 · 10 = 60 (см²)
Площадь сечения цилиндра, построенного параллельно его оси на расстоянии 4 см от нее, равна 60 см².
#SPJ1