Алгебра даю 100 баллов!
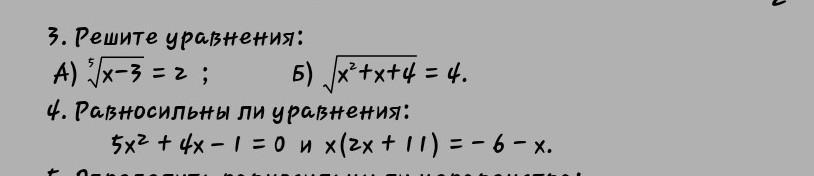
Ответы
3.А)
Возведем обе части уравнения в 5-ую степень:
Ответ: 35
3.Б)
Выражение, стоящее под знаком квадратного корня, должно быть неотрицательным.
Возведем обе части уравнения в квадрат:
На этом шаге видно, что выражение, стоящее под знаком квадратного корня, действительно неотрицательно.
Ответ: -4; 3
4)
Равносильными называются уравнения, множества решений которых совпадают.
Рассмотрим первое уравнение:
Решить уравнение можно через дискриминант, а можно заметить, что сумма старшего коэффициента и свободного члена равна второму коэффициенту.
В этом случае, первый корень уравнения равен -1:
А второй равен отношению свободного члена к старшему коэффициенту, взятому с противоположным знаком:
Рассмотрим второе уравнение:
Как видно, множества решений первого и второго уравнений не совпадают. Значит, они не равносильны.
Ответ: нет, не равносильны