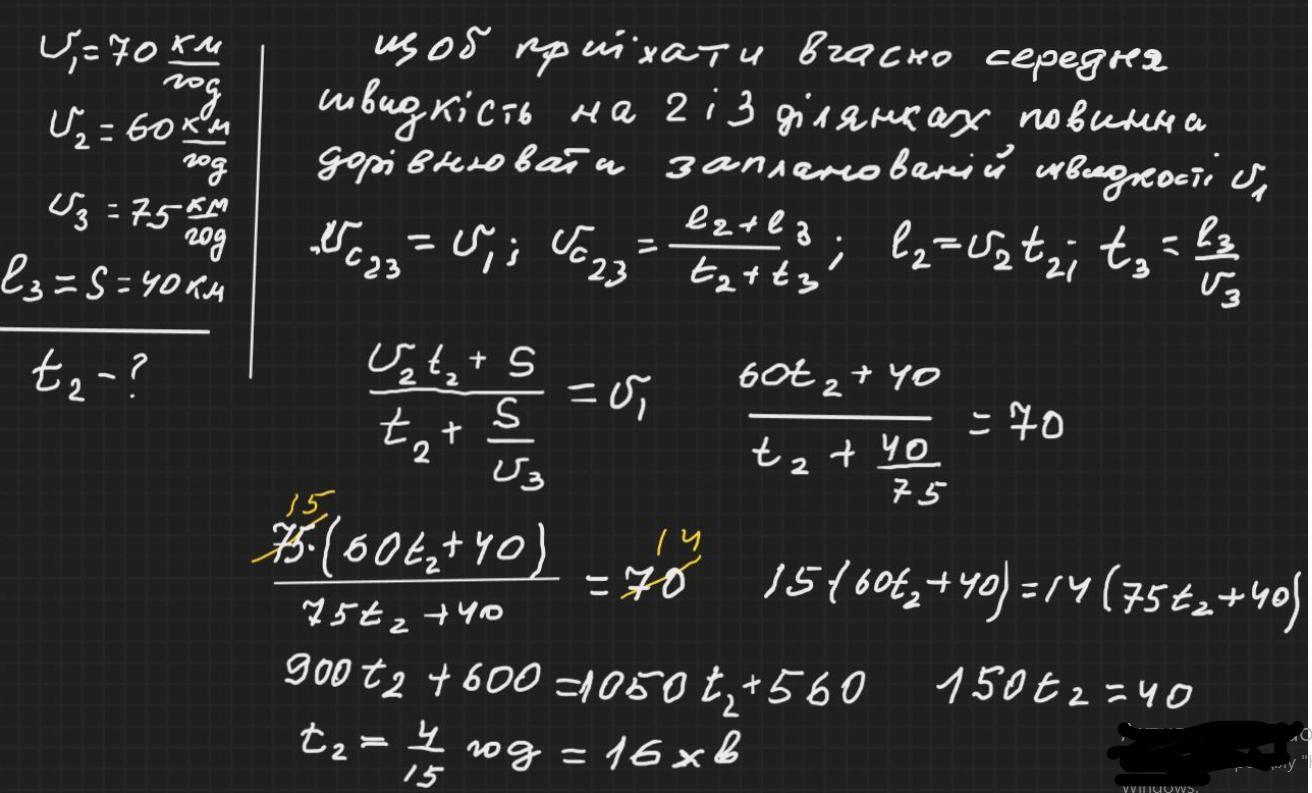Школярі поверталися з екскурсії на автобусі, який їхав зі швидкістю θ1 = 70
км/год. Пішов дощ, і водій зменшив швидкість до θ2 = 60 км/год. Коли дощ
скінчився, до школи залишалося проїхати S = 40 км. Автобус поїхав зі
швидкістю θ3 = 75 км/год і в'їхав на подвір'я школи в точно запланований
час. Скільки часу йшов дощ? Чому дорівнює середня швидкість автобуса?
Вважайте, що автобус в дорозі не зупинявся.
За повне розв'язання даю 100 балов
Ответы
Ответ:
Дано:
V₁ =70 км/год
V₂ = 60 км/год
V₃ = 75 км/год
S = 40 км
Найти: t - ?
Оскільки відстань від місця екскурсії до школи через дощ не змінилась, і час, при зменьшенні швидкості не змінився то середня швидкість співпадає з початковою швидкістю - 70 км/год.
Нехай дощ йшов протягом часу - t. Тоді шлях, що був пройдений за цей час, дорівнює V₂ * t км. Час, протягом якого після дощу автобус проїхав відстань, що залишилась, дорівнює S/V₃ год. Час витрачений автобусами з моменту початку дощу до прибуття в школу, повинен бути рівним часу, що необхідний для подолання тієї самої відстані з початковою швидкістю V₁:
t + (S/V₃) = (V₂ * t + S)/V₁ → t = (V₁/V₁ - V₂) * (S/V₁ - S/V₃) →
t = (S *(V₃ - V₁))/V₃(V₁ - V₂ )= (40 *(75 - 70))/75 *(70 - 60) = 200/750 = 4/15 год
4/15 год = 60 : 15 * 4 = 16 хв.
Відповідь: 16 хв
Пояснення: Оскільки автобус в'їхав на подвір'я школи в точно запланований час, то середня швидкість автобуса дорівнює запланованій швидкості ʋ1 = 70 км/год.