Предмет: Математика,
автор: xxflapsxx
При яких значеннях параметра a один з коренів рівняння ax^2+3(a+2)x-a=0 менший, а другий білший за 2
Приложения:
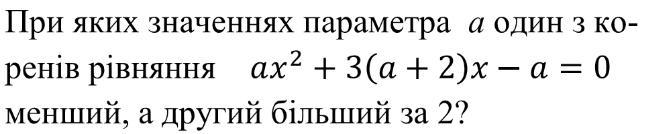
Ответы
Автор ответа:
1
Ответ:
ax^2+3(a+2)x-a=0
x^2+3(a+2)x/a-a/a=0
x^2+3(a+2)x/a-1=0
По условию x1=x2+2
тогда по т. Виета
(x2+2)x2=-1
(x2+1)²=1
x2=0
x1+x2==-3(a+2)/a
x2+2+x2=-3-6/a
2x2+5=-6/a
Т.к. x2=0
-6/a=5
a=-6/5
a=-1.2
Мог где-то что-то потерять. Потому обязательно перепроверяйте. Идея верная.
Пошаговое объяснение:
xxflapsxx:
Там же не больше на 2, а больше чем 2
Должно быть множество
Да, по условию все же x1<2, x2>2, потому можно отмечать ответ как неверный.
могу посоветовать тупо прописать через дискриминант оба корня, там где минус сделать меньше 2, а там где плюс больше. Но скорее всего красивых чисел не будет.
Похожие вопросы
Предмет: Литература,
автор: viktoria68163
Предмет: Алгебра,
автор: Pasheus
Предмет: Литература,
автор: yoshisupercell94
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: Аноним