Question

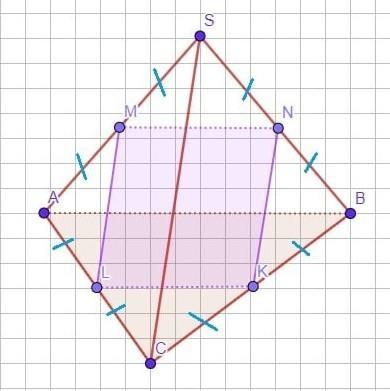
СРОЧНО!!!10. В тетраедрі SABC, всі ребра якого рівні, точки Μ, Ν, К, L — середини ребер AS, BS, BC, AC відповідно. Доведіть, що прямі МК і NL перетинаються під прямим кутом

Answer 1

Ответ:

Доведено, що MK⟂NL.

Объяснение:

В тетраедрі SABC всі ребра якого рівні, точки М, N, K, L – середини ребер AS, BS, BC, AC відповідно.Доведуть, що прямі MK і NL перетинаються під прямим кутом.

Теорія

• Середньою лінією трикутника називають відрізок, який сполучає середини двох сторін.

Властивість середньої лінії трикутника:

• Середня лінія трикутника, яка сполучає середини двох сторін, паралельна до третьої сторони і дорівнює ії половині.

РОЗВ’ЯЗАННЯ

SABC – тетраєдр. За умовою всі ребра тетраєдра рівні, тому усі грані – правільні трикутники.

Так як М, N, K, L – середини ребер AS, BS, BC, AC, то за означенням:

ML -  середня лінія трикутника ASC

MN - середня лінія трикутника ASB

NK – середня лінія трикутника BSC

LK – середня лінія трикутника ABC

Тому за властивістю середньою лінією трикутника:

ML || SC, NK ||SC. ML=NK=½•SC

MN || AB, LK || AB. MN=LK=½•AB.

Так як SC=AB, то  ML=NK=MN=LK=½•АВ.

В чотирикутнику MNKL протилежні сторони попарно паралельні, тому MNKL – паралелограм .

В паралелограмі MNKL всі сторони рівні, тому MNKL – ромб.

MK⟂NL – як діагоналі ромба.

 

#SPJ1