Предмет: Математика,
автор: Nukuta2121
Докажите тождество.
Приложения:
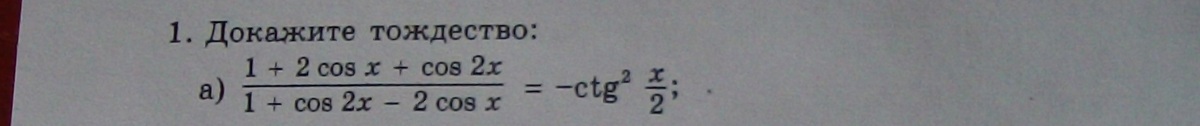
Ответы
Автор ответа:
0
1 + 2cos x + cos 2x = 1 + 2cos x + 2cos^2 x - 1 = 2cos^2 x + 2cos x
1 - 2cos x + cos 2x = 1 - 2cos x + 2cos^2 x - 1 = 2cos^2 x - 2cos x
(1 + 2cos x + cos 2x) / (1 - 2cos x + cos 2x) =
= (1 + 2cos x + 2cos^2 x - 1) / (1 - 2cos x + 2cos^2 x - 1) =
= (2cos^2 x + 2cos x) / (2cos^2 x - 2cos x) = (cos x + 1)/(cos x - 1) =
= - (1 + cos x)/(1 - cos x) = - [1 + 2cos^2(x/2) - 1] / [1 - 1 + 2sin^2(x/2)] =
= - (2cos^2(x/2)) / (2sin^2(x/2)) = - (cos(x/2) / sin(x/2))^2 = -ctg^2 (x/2)
1 - 2cos x + cos 2x = 1 - 2cos x + 2cos^2 x - 1 = 2cos^2 x - 2cos x
(1 + 2cos x + cos 2x) / (1 - 2cos x + cos 2x) =
= (1 + 2cos x + 2cos^2 x - 1) / (1 - 2cos x + 2cos^2 x - 1) =
= (2cos^2 x + 2cos x) / (2cos^2 x - 2cos x) = (cos x + 1)/(cos x - 1) =
= - (1 + cos x)/(1 - cos x) = - [1 + 2cos^2(x/2) - 1] / [1 - 1 + 2sin^2(x/2)] =
= - (2cos^2(x/2)) / (2sin^2(x/2)) = - (cos(x/2) / sin(x/2))^2 = -ctg^2 (x/2)
Автор ответа:
0
Спасибо!
Похожие вопросы
Предмет: География,
автор: lidiyakovaleva4
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: mrsybojestvo
Предмет: Литература,
автор: 5РИМ
Предмет: Химия,
автор: ruslanseidov9