Предмет: Алгебра,
автор: annachanqw0
доведіть тотожність
Приложения:
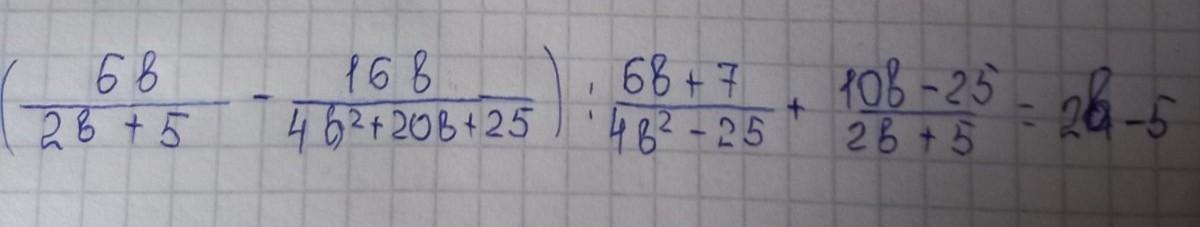
Ответы
Автор ответа:
1
Что и требовалось доказать
Похожие вопросы
Предмет: Химия,
автор: sevcenkomihajlo01
Предмет: Математика,
автор: necaevamergarita
Предмет: Литература,
автор: sofiakireeva158
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Английский язык,
автор: Pokoril