Предмет: Алгебра,
автор: olsanaviktoria
3*. Довести тотожність: ба 16a 2a+5 42 + 20 + 25 6a+7 4a²-25 + 10a-25 2a+5 = 2а-5
Даю 100 балів
Приложения:
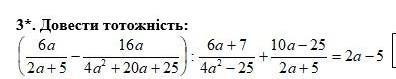
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: crocodiles88800
Предмет: Қазақ тiлi,
автор: raffirepro
Предмет: Литература,
автор: shevchenko2125
Предмет: География,
автор: vikusyavikusya1996
Предмет: Математика,
автор: vikmel21