найдите наиименьшее значение параметра а при котором график функции f(x) = 2/x и g(x) =ax+6 пересекаются в двух различных точках
Ответы
1) Решение аналитическое (только оно позволяет найти конкретный ответ, правда для указанных 1-4 классов вряд ли оно по силам)
f(x) = 2/x
g(x) =ax+6
Функции пересекаются - значит в этих точках их значения равны. Чтобы найти эти точки, функции приравнивают друг другу, получая уравнение:
ax + 6 = 2/x
ax + 6 - 2/x = 0 | *x (x ≠ 0)
ax² + 6x - 2 = 0
При решении квадратного уравнения часто сначала находят дискриминант - по нему можно сказать, сколько корней будет у уравнения (а значит и сколько будет точек пересечения наших функций):
D = b² - 4ac = 6² - 4*a*(-2) = 8а + 36
при D < 0 -нет корней
при D = 0 -один корень
при D > 0 -два корня
Нам нужно два корня, поэтому составляем неравенство, где дискриминант больше нуля:
8а + 36 > 0
8a > -36 | :8
a > -4,5
Так как вопрос был про наименьшее значение a, то в дробных числах ответ в виде одного числа дать не получится, можно лишь написать, что a → -4,5⁺ (то есть, ответом будет: "при a стремящемся к минус четырём с половиной справа"). Другими словами, когда a чуть больше, чем -4,5. Тут под фразой "чуть больше" имеется ввиду, что -4,5 и наше искомое число отличаются на бесконечно малую величину, и по идее можно записать наше искомое число в виде бесконечной десятичной периодической дроби -4,4(9).
Если же в задаче всё же написано дать целое значение a, то просто берём ближайшее целое, которое больше чем -4,5. Получим a = -4.
Ответ в общем случае: a → -4,5⁺
Ответ в целых числах: a = -4
2) Графическое решение (может дать приближённый ответ, либо ответ в целых числах - может быть как раз про целый ответ и было написано в исходной задаче?)
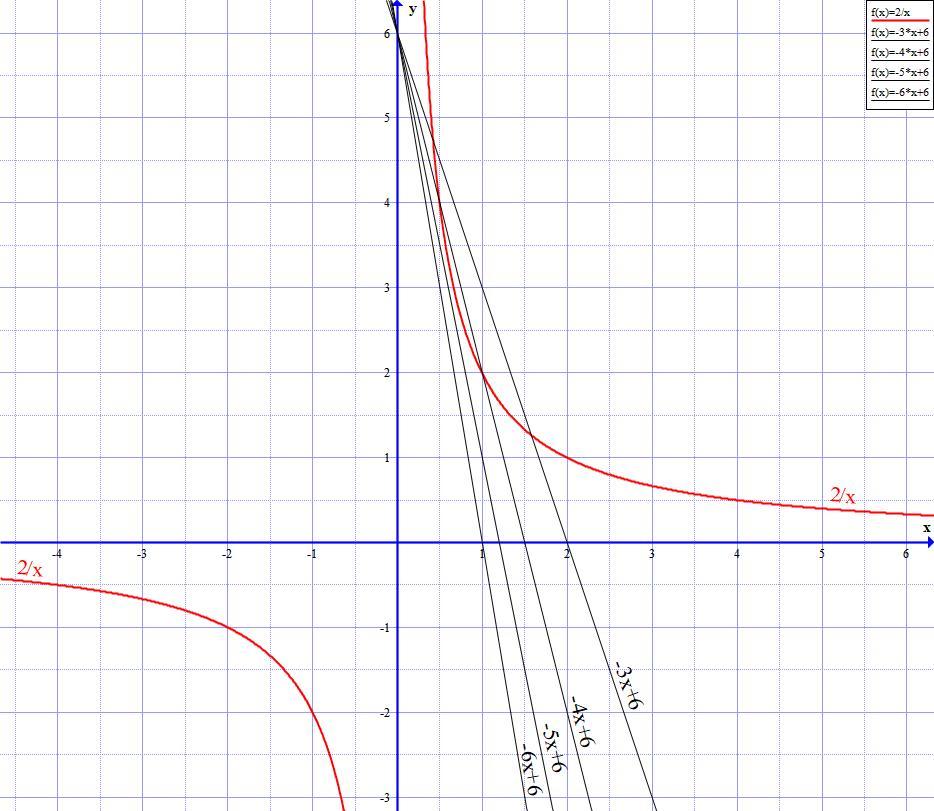
Строим график функции 2/x
Потом строим графики функции ax + 6 при разных значениях a (это будет несколько прямых линий с разным наклоном и одной общей точкой)
Если решать в целых числах, то по графикам будет видно, что наименьшее целое a, при котором есть два пересечения графиков - это a = -4 (смотри мой график внизу)
Если увеличивать точность, то можно строить графики функции ax + 6 через меньшие промежутки по a (например, через 0,1). Тогда можно увидеть, что при a = -4,5 графики касаются друг друга в одной точке, а уже при чуть большем значении (при a = -4,4) - уже пересекаются в двух точках. По идее, увеличивая точность таким образом, можно получить более точное значение a (например a = -4,49), однако бесконечно увеличивать точность таким образом не получится.
Поэтому, тут я укажу только ответ в целых числах: a = -4