Предмет: Алгебра,
автор: Аноним
Докажите, что при любых значениях а верны неравенства:
1 + (3a + 1)2 > (1 + 2a)(1 + 4a);
(3a – 2)(a + 2) < (1 + 2a)2.
Ответы
Автор ответа:
0
1)
1 + (3a + 1)² > (1 + 2a)(1 + 4a)
9a²+6а+2>1+6a+8a²
a²+1>0
2)
(3a – 2)(a + 2) < (1 + 2a)²
3a²+4a-4<4a²+4a+1
а²+5>0
3) Любое число в квадрате - положительное число. А сумма положительных чисел всегда >0
1 + (3a + 1)² > (1 + 2a)(1 + 4a)
9a²+6а+2>1+6a+8a²
a²+1>0
2)
(3a – 2)(a + 2) < (1 + 2a)²
3a²+4a-4<4a²+4a+1
а²+5>0
3) Любое число в квадрате - положительное число. А сумма положительных чисел всегда >0
Автор ответа:
0
Если понравилось решение - нажимай "спасибо" и "лучший" (рядом с кнопкой "спасибо") :)
Приложения:
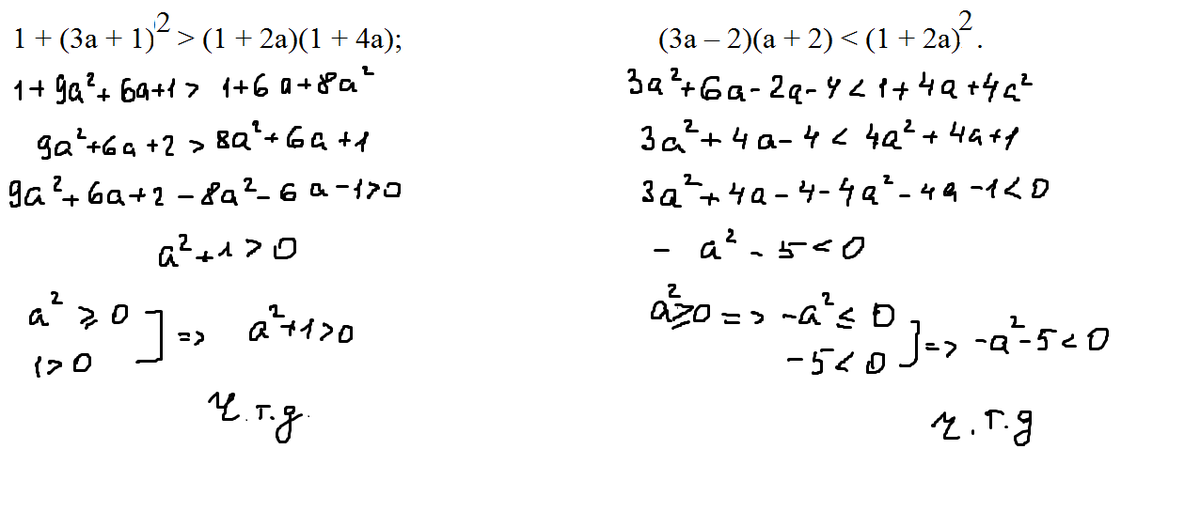
Похожие вопросы
Предмет: Литература,
автор: nsrakova
Предмет: География,
автор: Аноним
Предмет: Русский язык,
автор: urijderlys
Предмет: Алгебра,
автор: Pollinaria
Предмет: История,
автор: gvantza2010