Question

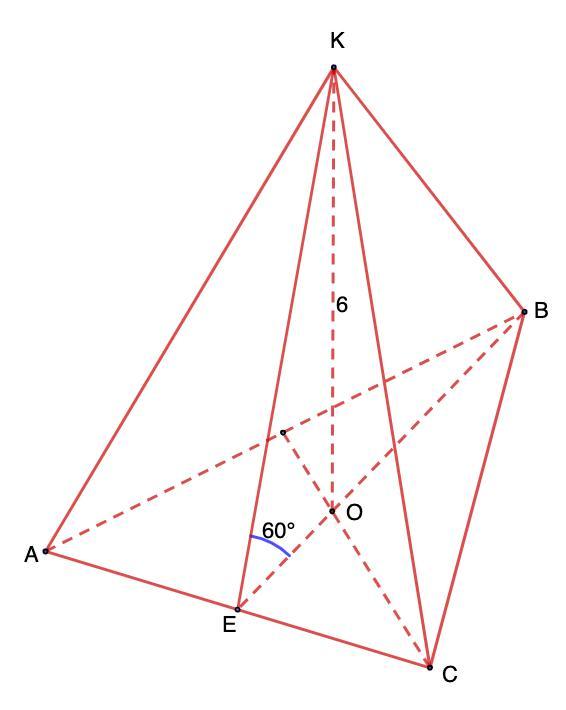
6. Бічна грань правильної трикутної піраміди утворює з площиною основи кут 60о, висота піраміди дорівнює 6см. Обчисліть повної площу поверхні піраміди.

Answer 1

Ответ:

Площадь полной поверхности пирамиды равна 108√3 см.

Объяснение:

6. Боковая грань правильной треугольной пирамиды образует с плоскостью основания угол 60°, высота пирамиды равна 6 см. Вычислите полной площадь поверхности пирамиды.

Дано: КАВС - правильная пирамида.

Угол наклона боковой грани к основанию = 60°;

КО = 6 см - высота.

Найти: Sполн.

Решение:

• В основании правильной треугольной пирамиды лежит равносторонний треугольник.

Sполн. = Sосн. + Sбок.

Sосн. = $\displaystyle \frac{a^2\sqrt{3} }{4}$ , где а - сторона основания.

Sбок. = $\displaystyle \frac{1}{2}Pl$ , где Р - периметр основания, l - апофема.

• В равностороннем треугольнике медианы являются высотами.

⇒ ВЕ - медиана, высота.

ВЕ ⊥ АС.

• Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной.

⇒ КЕ ⊥ АС.

⇒ углом наклона боковой грани к основанию будет ∠КЕВ = 60°.

Найдем апофему.

Рассмотрим ΔЕКО - прямоугольный.

КО = 6 см.

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sin\angle{KEO}=\frac{KO}{KE} \\\\KE=\frac{6}{sin\;60^0}=\frac{6\cdot2}{\sqrt{3} } =4\sqrt{3}$  (см)

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\angle{KEO}=\frac{EO}{KE} \\\\OE=KE\cdot cos\;60^0=4\sqrt{3}\cdot \frac{1}{2}=2\sqrt{3}$  (см)

• Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 : 1, считая от вершины.

⇒ ЕВ = ОЕ · 3 = 6√3 см

Найдем сторону основания.

• В равностороннем треугольнике все углы равны 60°.

$\displaystyle sin\;\angle{C}=\frac{BE}{BC}\\ \\\frac{\sqrt{3} }{2} =\frac{6\sqrt{3} }{BC}\\ \\BC=\frac{2\cdot 6\sqrt{3} }{\sqrt{3} }=12$ (см)

Площадь основания равна:

Sосн. = $\displaystyle \frac{12^2\sqrt{3} }{4} =36\sqrt{3}$ (см²)

Периметр основания равен:

Р = 12 · 3 = 36 (см)

Теперь найдем площадь полной поверхности:

Sполн. = $\displaystyle 36\sqrt{3}+\frac{1}{2}\cdot 36\cdot 4\sqrt{3} =36\sqrt{3}+72\sqrt{3}=108\sqrt{3}$ (см²)

Площадь полной поверхности пирамиды равна 108√3 см.

#SPJ1