Предмет: Математика,
автор: varvaradoronina268
найдите корнь уравнение x²-4|x|+3=0 которое удовлетворяет неравенству |x+1|_<3,5
Приложения:
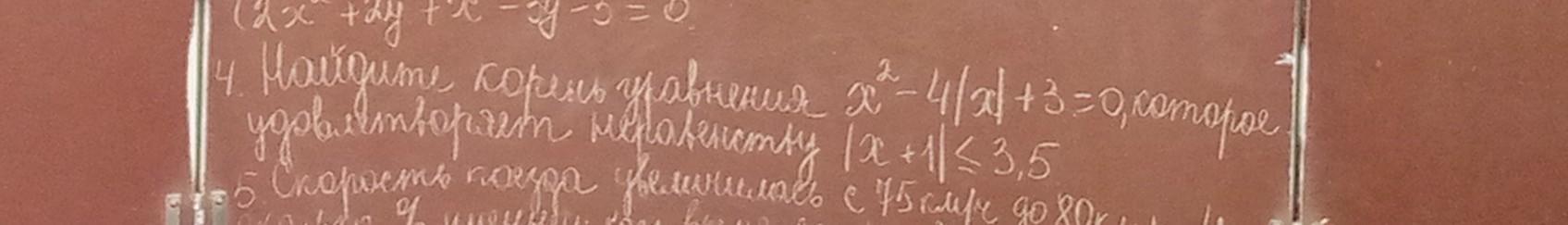
Ответы
Автор ответа:
1
Ответ:
х2 = 1
Пошаговое объяснение:
x²-4|x|+3=0 - решаем через дискриминант
a = 1, b = -4, c = 3
D = b² - 4ac = 16 - 12 = 4 ⇒ D>0 значит уравнение имеет 2 корня
х1 = - b + /2а = - (-4) + 2/ 2*1 = 6/2 = 3
х2 = - b - /2а = - (-4) - 2/ 2*1 = 2/2 = 1
|x+1|<3,5 = |3+1|<3,5 = 4 > 3,5 - решение не удовлетворяет неравенству.
|x+1|<3,5 = |1+1|<3,5 = 2 <3,5 - решение удовлетворяет неравенству.
х2 = 1 - является корнем уравнения.
Похожие вопросы
Предмет: Немецкий язык,
автор: leshapapovich6
Предмет: Геометрия,
автор: sluba8651
Предмет: Химия,
автор: 00pelmeshka00
Предмет: Математика,
автор: dasamur00