Question

Дайте ответ на задачу на фото

Answer 1

Ответ:

Доказано, что AB || CD.

Объяснение:

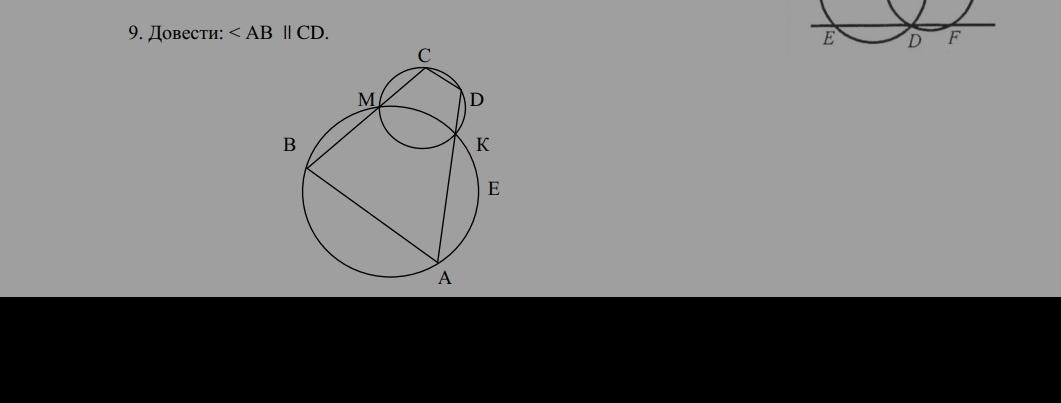
Задача по готовому чертежу.

Доказать, что AB || CD.

Решение:

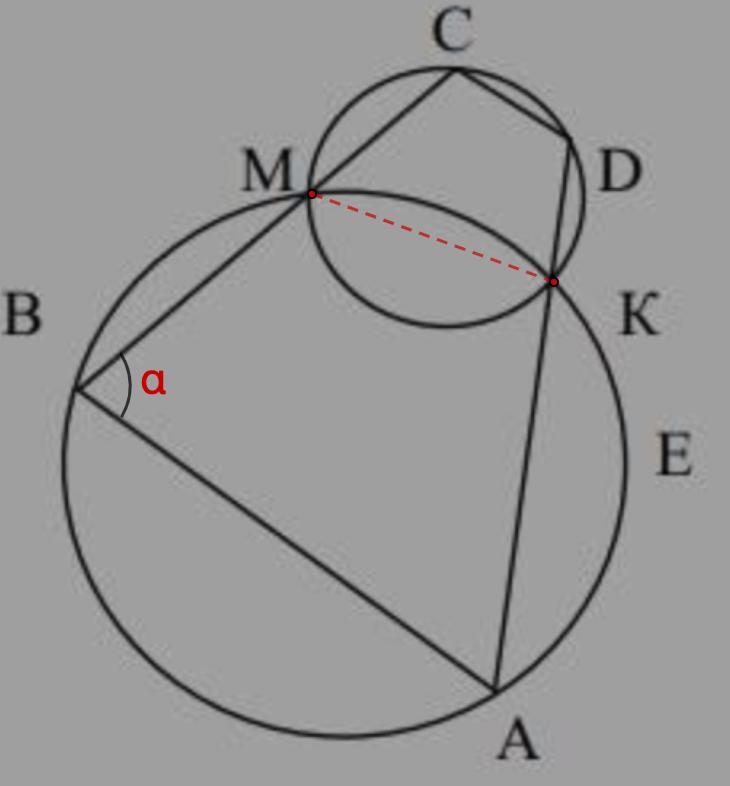
Соединим М и К.

• Четырёхугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180°.

Рассмотрим ВМКА - вписанный.

Пусть ∠В = α, тогда ∠МКА = 180° - α

• Сумма смежных уголов равна 180°.

⇒ ∠MKD = 180° - ∠MKA = 180° - 180° + α = α

Рассмотрим МСDK - вписанный.

∠МКD + ∠C = 180°

⇒ ∠C = 180° - ∠МКD = 180° - α

∠B + ∠C = α + 180° - α = 180° - внутренние односторонние при CD и АВ и секущей ВС.

• Если при пересечении двух прямых третьей сумма односторонних углов равна 180°, то эти прямые параллельны.

⇒ AB || CD.