Предмет: Геометрия,
автор: kostagribinnik213
Діагональ трапеції ділить середню лінію на відрізки,один з яких у два рази більший від другого. Знайти основи трапеції , якщо її середня лінія 42 см
Ответы
Автор ответа:
2
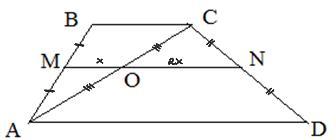
Дано: АВCD - трапеция, MN - средняя линия, АС - диагональ, т.О ∈ MN, ON=2MO, MN= 42 см.
Найти: ВС, АD.
Решение.
Поскольку диагональ делит среднюю линию на отрезки, один из которых в два раза больше другого, то обозначим МО=х, ON , соответственно, 2х. Тогда:
х+2х=42;
3х= 42;
х=МО= 14 (см)
Тогда ON= 2MO= 14•2= 28 (см)
Средняя линия трапеции проходит через середины диагоналей , т.е. т.О делит АС пополам, соответственно АО=ОС. (Этот факт можно было бы доказать по теореме Фалеса)
Известно, что средняя линия треугольника, отсекает треугольник, подобный данному с коэффициентом ½. Отсюда:
В ΔACD:
AD= 2ON= 2•28= 56 (см).
В ΔВАС:
ВС= 2•МО= 2•14= 28 (см).
Ответ: 56 см, 28 см.
Рисунок приложен.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: denkof1
Предмет: Математика,
автор: Locvi
Предмет: Английский язык,
автор: hoopgood05
Предмет: Английский язык,
автор: dilyaraoral221202
Предмет: Математика,
автор: Аноним