Предмет: Алгебра,
автор: blyasha
вычислить указанный интеграл
Приложения:
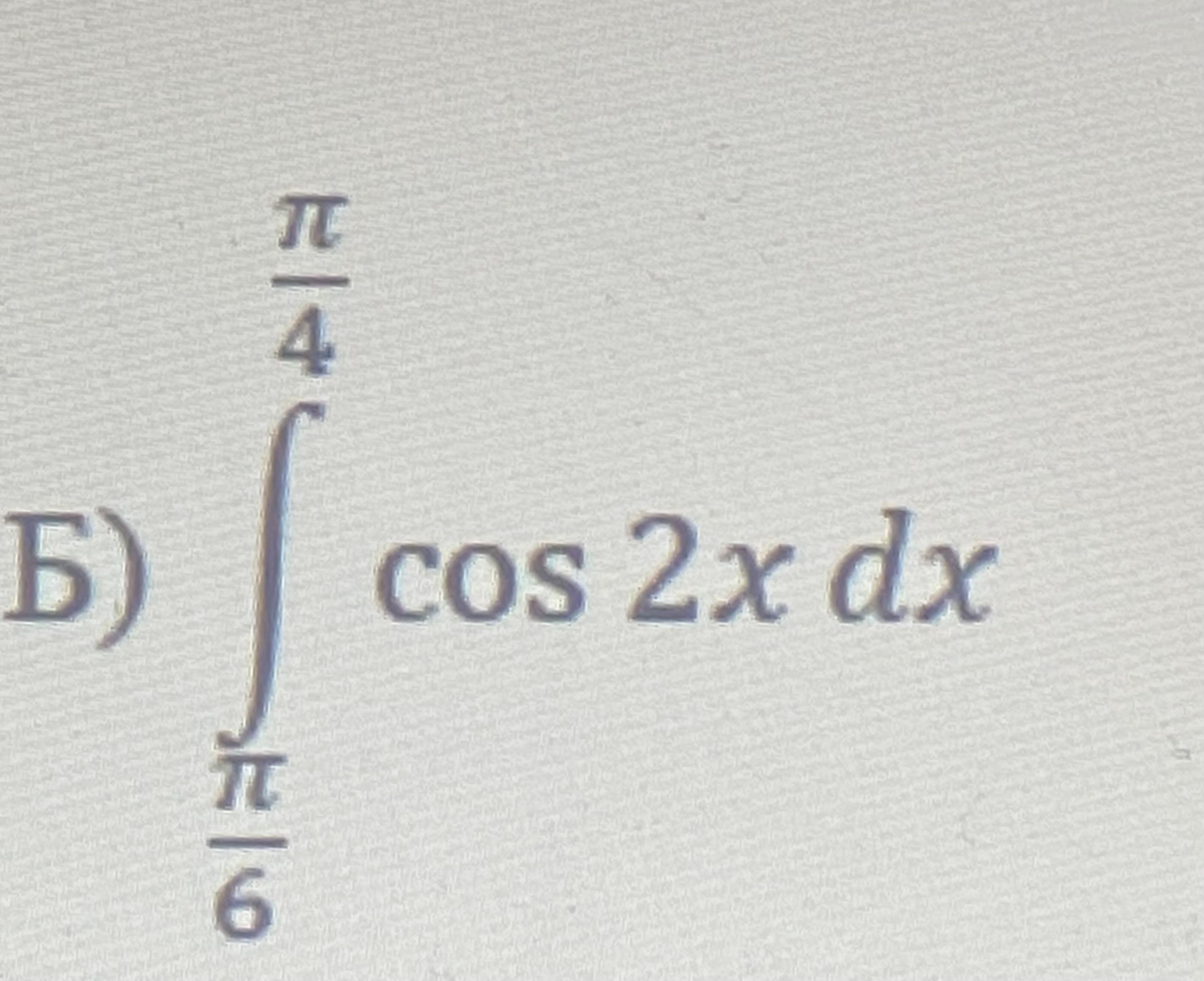
Ответы
Автор ответа:
1
Ответ:
1/2 - корень из 3/4
Объяснение:
на
Приложения:

Автор ответа:
0
Решение.
Для вычисления определённого интеграла применяем метод замены переменной и формулу Ньютона-Лейбница .
Похожие вопросы
Предмет: Химия,
автор: bot898025
Предмет: Информатика,
автор: teregkova2
Предмет: Математика,
автор: istvan95
Предмет: Математика,
автор: movlyan20071981
Предмет: История,
автор: vika22246