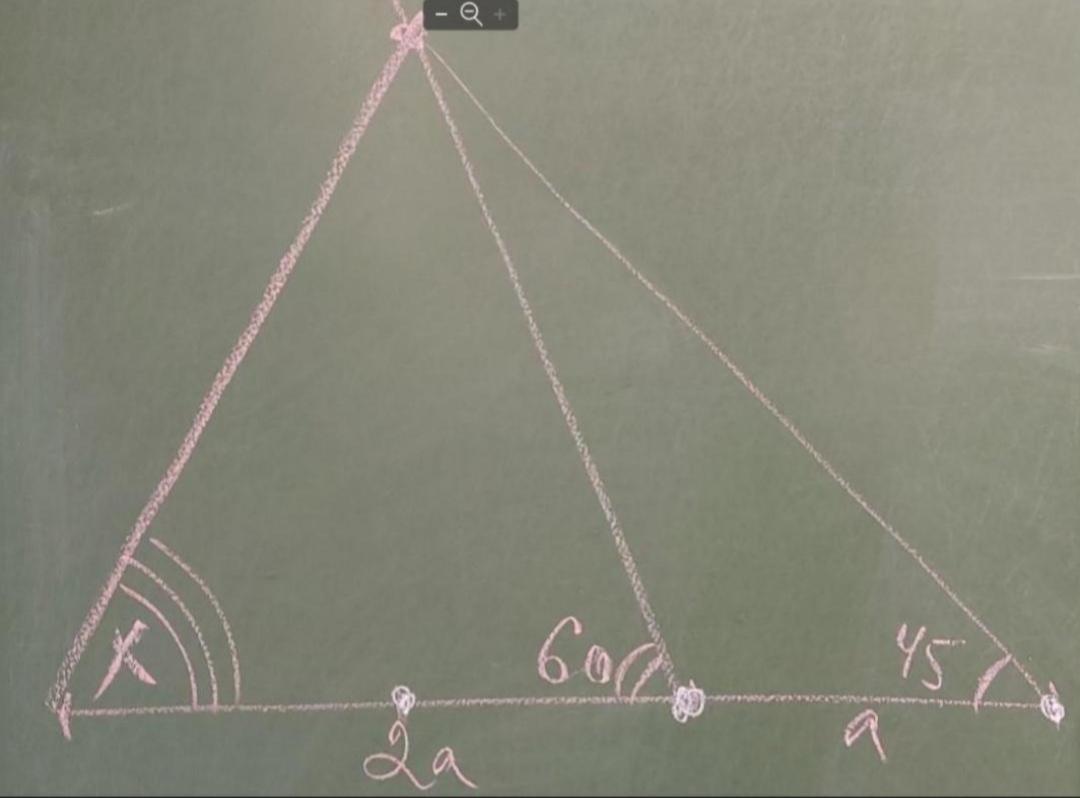
Предмет: Геометрия, автор: zmeura1204

Квест продолжается.... Найти угол х. Без тригонометрии. Задача 7 класса.

Приложения:

cos20093: То есть три точки B, C и X лежат на одной прямой, причем CX = 2*CB. И каждая соединена с точкой A вне этой прямой так, что ∠ABX = 45° ∠ACX = 60°; Над найти ∠AXB. С условием покончено, теперь решение :). В △ABC AC/AB = sin(45°)/sin(180° - 60°) = √(2/3); здесь важно, что это свойство никак не связано с точкой X, а определяется только треугольником ABC.

cos20093: Следующий шаг - очевидно, что площадь △AXC составляет 2/3 от площади △AXB - так как CX/BX = 2/3, а высота к ЭТОЙ стороне - общая. Если теперь провести высоты из точки X к AC и AB, то отношение этих высот будет равно (2/3)/√(2/3) = √(2/3); то есть точно такое же, как и отношение сторон, к которым они проведены. В этом кроется "разгадка" выбора точки X на прямой BC на расстоянии именно CX = 2*CB;

cos20093: Кроме пропорциональности сторон и высот, важно еще и то, что эти стороны видны под одинаковыми углами ( под одним и тем же углом AXB). Такие треугольники обязательно подобны, что можно доказать разными способами, в том числе заметить, что высота равна боковой стороне (с которой она имеет общую вершину), умноженной на синус угла напротив высоты. То есть есть еще одна пропорциональная пара сторон и общий угол между ними. Другой способ есть в одном из предыдущих комментариев.

cos20093: Предыдущий комментарий неверен, прошу прощения. Верный способ рассуждения - если мысленно увеличить стороны меньшего треугольника ACX в √(3/2). Стороны напротив общего угла AXB станут равными и высоты к ним - равными, так как площади тоже станут равными. Далее все очевидно :) Забавное рассуждение. Как видите, я сам его понимал не до конца четко :) попытка упростить увела с правильной дорожки. :)

cos20093: Почему же треугольники станут равными? Если у двух треугольников равны стороны и высоты к ним, то они не обязаны быть равными - равны только площади. Но если есть еще одно условие - стороны видны из вершины под одинаковым углом, то равенство обязательно. Вершина будет в точке пересечения прямой, параллельной основанию и отстоящей от неё на длину высоты и окружности, из которой сторона видна под заданным углом. Таких точек только две, и в обоих случаях треугольники равны.

cos20093: Может показаться странным, что у треугольников уже есть стороны, отношение у которых 2/3, а не √(2/3). Фокус в том, что это не соответствующие стороны :). Стороне CX в △ACX соответствует не BX, а AX в △ABX. Сторона же BX соответствует той же AX, но уже в △ACX. То есть CX/AX = AX/BX = k; поэтому CX/BX = k², где k - коэффициент подобия △ABX и △ACX, равный √(2/3);

cos20093: Ну, и вишенка на всей этой куче слов :) - показать, что AC/AB = √(2/3); можно без теоремы синусов. Надо просто опустить перпендикуляр из A на BX и выразить его через AC и AB по теореме Пифагора. Уж это 7-классники знают.

cos20093: Я нашел еще одно, очень красивое решение через вписанные углы. Но это будет секретно :)

cos20093: чисто геометрическое

zmeura1204: Можете выложить, я не в 7 классе.

Ответы

Автор ответа: cos20093

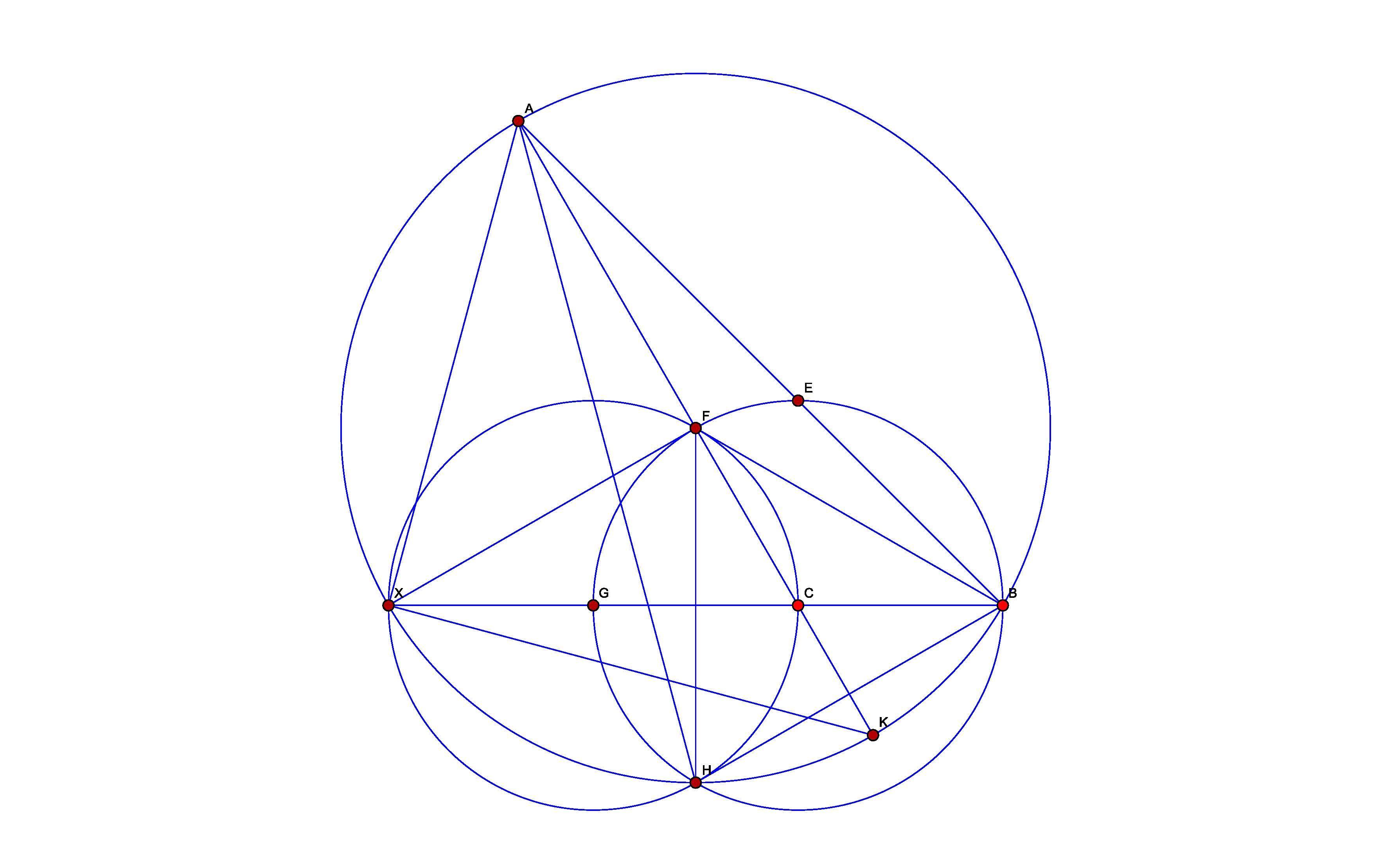
См. чертеж. Все решение заключается в порядке построений этого чертежа.

1) Строятся две одинаковые окружности с центрами в точках C и G. Линия центров пересекает эти окружности в точках B и X.

2) Четырехугольник XFBH - ромб, составленный из 2 правильных треугольников. Ну, в смысле, FX = FH = FB. Поэтому через точки X H и B проходит окружность с центром в точке F.

3) Прямая CF образует с XB угол 60° (так как CFG тоже правильный треугольник, просто по построению.

4) Пусть эта прямая пересекает окружность (XBH) в точке A. Я хочу в рамках этого построения найти ∠AXB и ∠ABX. (то есть я немного изменил условие задачи, потом вернусь к первоначальному).

5) Углы находятся очень просто. Для начала, центральный угол дуги XB окружности (XBA) ∠XFB = 120°; => ∠XAB = 60°;

Далее, линия центров CF окружностей (HBF) и (HBA) (на которой по построению лежит точка A), очевидно перпендикулярна общей хорде HB, делит пополам её и стягиваемую ею дугу, и вообще является осью симметрии для этой пары окружностей. То есть точка K - середина дуги HB большей окружности. Возвращаясь к пункту 2) построения, ∠HXB = 30°, => ∠KXB = 15°. Но KA - диаметр большей окружности, ∠KXA = 90°; => ∠AXB = 90°-15 = 75°;

Ну, и ∠ABX = 180° - 60° - 75° = 45°;

Теперь можно вернуться к исходной задаче. Ясно, что исследованная конструкция совпадает с условием - ввиду подобия треугольников с заданными углами в 120° и 45°, а также СX = 2*CB; собственно, это все.

Приложения: