Предмет: Математика,
автор: mika82723
Помогите пожалуйста, даю 50 баллов
Приложения:
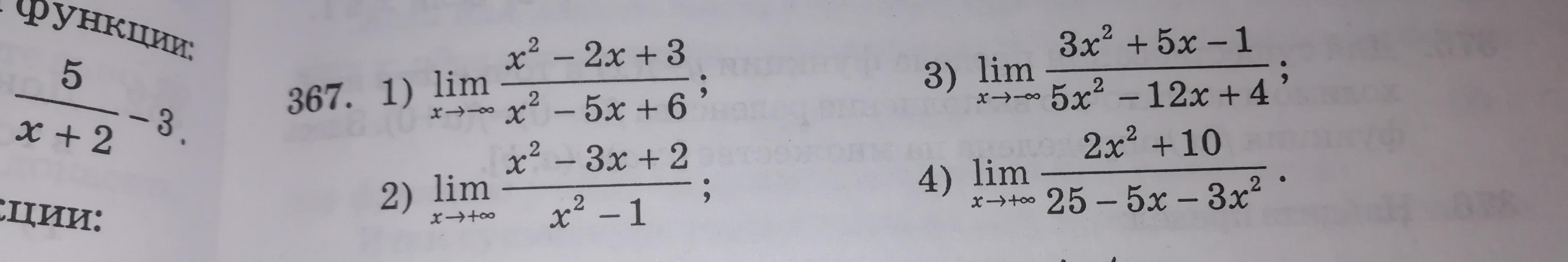
Ответы
Автор ответа:
1
Ответ:
1)
2)
3)
4)
Объяснение: во всех пределах имеем с неопределенностью типа ∞/∞. Поэтому из каждой части дроби выводим за скобки старшую степень и сокращаем их. После этого ставим значение х, к которому оно стремится.
1)
2)
3)
4)
Похожие вопросы
Предмет: Право,
автор: polikrovska38
Предмет: Математика,
автор: misabiloborodov
Предмет: Немецкий язык,
автор: bbebrovna70
Предмет: Алгебра,
автор: sofiyagatilova